Случайная величина х задана функцией плотности: .
Найти: а) коэффициент С, б) функцию распределения 
; в) вероятность попадания случайной величины на интервал 
; г) математическое ожидание и дисперсию.
При наборе телефонного номера абонент забыл последнюю цифру, но помнит, что она нечетная.
Составить закон распределения числа попыток, сделанных абонентом для первичного набора номера. Найти математическое ожидание и дисперсию этой случайной величины.
Длина изготовляемой автоматом детали представляет собой случайную величину, распределенную по нормальному закону с параметрами 
см и 
см.
Какую точность длины изготовленной детали можно гарантировать с вероятностью 0,9758?
Лифт в 5-ти этажном доме отправляется с 3 пассажирами.
Найти вероятность того, что на каждом этаже выйдет не более одного пассажира, предполагая, что все возможные способы распределения пассажиров по этажам равновероятные.
В ящике лежат 8 красных, 10 зеленых и 12 синих шаров, одинаковых на ощупь. Наугад вынимают 3 шара.
Какова вероятность того, что: а) хотя бы два из них одного цвета; б) два из них красных, а один синий.
Из 10 деталей 4 окрашены. Вероятность того, что окрашенная деталь тяжелее нормы равна 0,3, а для неокрашенной детали эта вероятность равна 0,1. Взятая наугад деталь оказалась тяжелее нормы.
Найти вероятность того, что она окрашена.
Всхожесть семян некоторого растения составляет 70%.
Какова вероятность того, что из 10 посеянных семян: а) взойдут восемь; б) взойдут по крайней мере 8?
Вероятность поражения мишени стрелком при одном выстреле равна 0,8.
Найти вероятность того, что при 100 выстрелах мишень будет поражена не менее 86 и не более 100 раз.
Плотность распределения случайной величины Х имеет вид: 
.
Определить: а) коэффициент А; б) функцию распределения 
; в) вероятность попадания случайной величины на интервал (-1; 1); г) математическое ожидание и дисперсию.
Часовщик, желая найти требующие ремонта часы, проверяет их до обнаружения I-х неисправных.
Составить закон распределения числа просмотренных часов, если известно, что среди имеющихся 10 часов 6 неисправны. Найти математическое ожидание и дисперсию этой случайной величины.
На автомате изготавливают заклепки. Диаметр их головок представляет случайную величину Х, распределенную по нормальному закону с параметрами 
мм и 
см 2 .
Найти вероятность брака, если допустимые размеры головок 2±0,05 мм.
Обезьянке позволили семь раз ударить по клавишам пишущей машинки (для упрощения считаем, что на клавиатуре машинки 33 буквы русского алфавита и 10 цифр).
Найти вероятность того, что она напечатает слово “ЧЕЛОВЕК”.
В конверте восемь мужских и две женские фотографии. Из конверта берут четыре фотографии.
Какова вероятность того, что из них: а) ровно две женские фотографии; б) хотя бы одна женская фотография?
В специализированную больницу поступают в среднем 70% больных заболеванием К, остальные – М. Вероятность полного излечения болезни К равна 0,8, болезни М – 0,9. Больной, поступивший в больницу, был выписан здоровым.
Какова вероятность того, что он болен болезнью К.
Вероятность выиграть по одному билету лотереи равна 1/7.
Какова вероятность, имея 5 билетов выиграть: а) по всем пяти; б) хотя бы по одному билету.
Вероятность того, что шестерня механических часов имеет заусенцы, равна 0,3.
Найти вероятность того, что из 2100 шестерен, поступивших на сборку, не более 1479 имеют заусенцы.
Плотность распределения случайной величины Х задана графиком:
1. Написать выражение плотности распределения.
А 2. Найти функцию распределения и построить ее график.
3. Вычислить математическое ожидание и дисперсию Х.
Три цеха стекольного завода изготовляют продукцию в соотношении 9:8:3. Среди продукции первого цеха – 70% термостойкой, среди продукции второго цеха – 80%, среди продукции третьего цеха – 90%. Найти среднее значение и дисперсию числа термостойких изделий среди наудачу взятых 10 изделий.
На автомате изготавливают заклепки. Диаметр их головок представляет случайную величину Х, распределенную по нормальному закону с параметрами 
мм и 
см 2 .
Какие размеры диаметра головок заклепки можно гарантировать с вероятностью 0,9545?
Рабочий обслуживает 3 станка. Вероятность того, что в течение смены потребует его внимания первый станок, равна 0,7, второй – 0,75, третий – 0,8.
Найти вероятность того, что в течение смены потребуют внимания какие-либо два станка.
Студент выполняет контрольную работу в классе контролирующих машин. Работа состоит из 3 задач. Для получения положительной оценки достаточно решить две задачи. Для каждой задачи зашифровано 5 различных ответов, из которых только один правильный. Студент плохо знает материал и поэтому выбирает ответы для каждой задачи наудачу. Какова вероятность того, что он получит положительную оценку?
Найдите вероятность того, что среди них: а) не менее трех спелых; б) хотя бы один спелый.
Статистика запросов кредитов в банке такова:10% — государственные органы, 30% — другие банки, остальные – физические лица. Вероятность невозврата взятого кредита соответственно таковы: 0,01; 0,05 и 0,2.
Найти вероятность невозврата очередного запроса на кредит. Начальнику кредитного отдела доложили, что получено сообщение о невозврате кредита, но в факсовом сообщении имя клиента было плохо пропечатано. Какова вероятность, что данный кредит не возвращает какой-то банк?
В хлопке 70% длинных волокон.
Какова вероятность того, что среди взятых наугад 10 волокон: а) хотя бы одна длинная; б) 6 длинных?
Вероятность поражения мишени при одном выстреле равна 0,9.
Найти вероятность того, что при 100 выстрелах мишень будет поражена не менее 86 раз и не более 94 раз.
Случайная величина Х задана дифференциальной функцией: 
. Найти: а) коэффициент С; б) функцию распределения 
; в) вероятность попадания на интервал 
; г) математическое ожидание и дисперсию случайной величины Х.
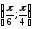
Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,005.
Составить первые 3 члена закона распределения числа опоздавших среди 1000 пассажиров некоторого поезда. Найти математическое ожидание и дисперсию этой случайной величины.
Источник
Функция распределения случайной величины. Непрерывная случайная величина. Плотность вероятности
Тема 6
Блок В
Блок А
Задачи для отчета преподавателю
А 5.1.Стрелок, имея 4 патрона, стреляет по удаляющейся цели до 1-го попадания или до израсходования всех патронов. Составить закон распределения числа произведенных выстрелов, если вероятность попадания при 1-м выстреле равна 0,8, а при каждом следующем уменьшается на 0,1.
А 5.2.Проверкой установлено, что из каждых десяти деталей, поступающих на сборку двигателя самолета, 2 нуждаются в доводке. Составить закон распределения числа точно изготовленных среди наудачу взятых 3 деталей. Найти математическое ожидание и дисперсию этой случайной величины.
А 5.3.Завод отправил на базу 100 000 доброкачественных керамических плиток. Вероятность того, что плитка в пути разобьется, равна 0,00007. Составить закон распределения числа поврежденных плиток, указав первые 4 его члена. Найти математическое ожидание и дисперсию этой случайной величины.
А 5.4.Каждый из 2 стрелков делает по 2 выстрела по мишени,
вероятность попадания в которую для 1-го стрелка равна 0,8, для
2-го – 0,9. Составить закон распределения общего числа попаданий.
А 5.5.На пути движения автомашины 3 светофора, каждый из которых может быть открыт с вероятностью 0,5. Составить закон распределения числа светофоров, пройденных автомашиной: а) до 1-й остановки; б) без остановки. Найти математическое ожидание каждой из этих случайных величин.
А 5.6.При наборе телефонного номера абонент забыл последнюю цифру, но помнит, что она нечетная. Составить закон распределения числа попыток, сделанных абонентом для правильного набора номера.
А 5.7.Часовщик, желая найти требующие ремонта часы, проверяет их до обнаружения 1-х неисправных. Составить закон распределения числа просмотренных часов, если известно, что среди имеющихся 10 часов 6 – неисправны.
А 5.8.В коробке имеются 6 однотипных деталей, из которых 2 –с дефектами. Для сборки прибора требуются 2 детали, которые слесарь-сборщик извлекает из коробки. Составить закон распределения числа опробованных для сборки прибора деталей. Найти
математическое ожидание и среднее квадратическое отклонение этой случайной величины.
А 5.9.Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,005. Составить первые 3 члена закона распределения числа опоздавших среди 1000 пассажиров некоторого поезда. Найти математическое ожидание и дисперсию этой случайной величины.
А 5.10.Среди 20 электроприборов имеются 2 неисправных. Составить закон распределения числа неисправных приборов среди 4 одновременно взятых приборов. Найти математическое ожидание и среднее квадратическое отклонение этой случайной величины.
А 5.11.Рабочий обслуживает 3 станка, вероятности выхода из строя каждого из которых в течение часа соответственно равны 0,2; 0,15; 0,1. Составить закон распределения числа станков, не требующих ремонта в течение часа. Найти математическое ожидание и дисперсию этой случайной величины.
А 5.12.В городе имеются 4 библиотеки. Вероятность наличия в данный момент нужной книги в каждой из библиотек равна 0,2. Составить закон распределения и найти среднее квадратическое отклонение числа посещенных студентом библиотек для получения нужной книги.
А 5.13.Два баскетболиста делают по 2 броска. Вероятность
попадания мяча в корзину при любом броске для 1-го баскетболиста равна 0,8, для 2-го – 0,9. Составить закон распределения общего числа попаданий.
А 5.14.Вероятность того, что саженец груши приживется, равна 0,8, яблони – 0,9. Куплено 2 саженца груши и 1 – яблони. Составить закон распределения числа прижившихся среди них.
А 5.15.Среди 10 приборов у 2 имеются отклонения, выходящие за пределы допуска. Составить закон распределения числа
приборов, не имеющих отклонений от допуска, среди 4 наудачу взятых приборов.
А 5.16.Число очков, выбиваемых стрелком при каждом выстреле, имеет следующий закон распределения:
| хi | ||||
| рi | 0,1 | 0,2 | 0,3 | 0,4 |
Найти математическое ожидание и дисперсию числа очков, выбиваемых стрелком, если он сделал 5 выстрелов.
А 5.17.По условиям спортивной игры стрельба по мишени ведется стрелком до 2 попаданий или до израсходования имеющихся 4 патронов. Составить закон распределения и найти математическое ожидание числа попаданий, если вероятность попасть при первом
выстреле равна 0,6, а при каждом следующем увеличивается на 0,1.
А 5.18.Вероятность успешно сдать экзамен по теории вероятности равна 0,8, а при каждой пересдаче увеличивается на 10%. Составить закон распределения числа попыток сдать экзамен, если студент может пересдавать экзамен не более 2 раз.
А 5.19.Продано 100 билетов лотереи. Установлены следующие выигрыши: 1 выигрыш – 15 тыс. грн, 2 выигрыша – по 10 тыс. грн,
и 5 выигрышей – по 5 тыс. грн. Составить закон распределения и найти математическое ожидание выигрыша для лица, купившего 1 билет.
А 5.20.При некотором технологическом процессе брак составляет в среднем 3%. Составить закон распределения числа стандартных изделий среди взятых наудачу 5 изделий этого производства.
А 5.21.Вероятность безотказной работы каждого станка в течение промежутка времени t равна 0,75. Найти вероятность того, что из 12 станков, обслуживаемых рабочим, внимания потребуют 4 станка.
А 5.22.Случайная величина Х задана законом распределения
| хi | ? | ||
| рi | 0,2 | 0,4 | ? |
Найти х3 и р3, если известно, что среднее значение случайной величины равно 2,4.
А 5.23.Торговая база получила 5000 электроламп. Вероятность повреждения электроламп в пути равна 0,001. Написать первые 5 членов закона распределения числа поврежденных электроламп.
А 5.24.Случайная величина Х принимает целые положительные значения с вероятностями, убывающими в геометрической прогрессии. Найти знаменатель этой прогрессии, если известно, что математическое ожидание этой случайной величины равно 10, а вероятность того, что она принимает значение 3, равна 0,081.
А 5.25.Вероятность того, что абонент позвонит по телефону в течении часа, равна 0,01. Телефонная станция обслуживает 1000 абонентов. Написать первые 3 члена закона распределения случайной величины – числа позвонивших абонентов в течение часа. Найти ее среднее значение.
А 5.26.Билет в партер стоит 4 грн, в бельэтаж – 3 грн и на балкон – 2 грн. Приобретения любого билета события равновозможные.
Составить закон распределения стоимости 2 купленных билетов.
А 5.27.Команда состоит из 2 биатлонистов, вероятность попадания в цель 1-м из которых равна 0,8, а 2-м – 0,9. По условию
соревнований – 1-й может сделать 1 выстрел, 2-му же, в случае промаха, разрешено сделать еще один выстрел. Составить закон распределения общего числа попаданий.
А 5.28.Из коробки, содержащей 7 окрашенных и 3 неокрашенных шара, извлекаются по 1 шару. Составить закон распределения числа неокрашенных шаров, извлеченных до появления 1-го окрашенного шара, и найти их среднее число. Рассмотреть 2 схемы опыта – извлеченный неокрашенный шар в коробку: а) не возвращается; б) возвращается перед новым извлечением.
А 5.29.Три цеха стекольного завода изготовляют продукцию в соотношении 9:8:3. Среди продукции 1-го цеха – 70% термостойкой, среди продукции 2-го цеха – 80%, среди продукции
3-го цеха – 90%. Найти среднее значение числа термостойких изделий среди наудачу взятых 10 изделий.
А 5.30.В ящике лежат 10 теннисных мячей, среди которых 6 новых и 4 играных. Из ящика извлекаются наугад 2 мяча для
игры, после чего возвращаются в ящик. После этого из ящика вновь извлекаются 2 мяча для следующей игры. Составить закон распределения числа новых среди взятых во второй раз мячей.
А 5.31.Длительной проверкой установлено, что из каждых 10 двигателей один нуждается в дополнительной регулировке. Составить закон распределения числа нуждающихся в дополнительной регулировке двигателей среди 3 взятых наудачу.
А 5.32.В автобусе 4 пассажира. Считается, что каждый из
пассажиров с равной вероятностью может сойти на любой из
оставшихся 3 остановок. Пусть Х означает число пассажиров,
сошедших на 1-й остановке. Написать закон распределения
случайной величины Х и найти ее числовые характеристики.
А 5.33.За некоторый промежуток времени амеба может погибнуть с вероятностью 1/4, выжить – с 1/4 и разделиться на две – с 1/2. В следующий такой же промежуток времени с каждой амебой независимо от ее «происхождения» происходит то же самое. Сколько амеб и с какими вероятностями может существовать к концу 2-го промежутка времени?
А 5.34.Всхожесть семян данного растения определяется вероятностью 0,6. Пусть X – число появившихся растений из 5 семян. Найти закон распределения X.
А 5.35.Случайная величина X принимает два значения: х1 = 4, х2 = 5, причем M(X) = 4,6. Найти закон распределения X.
А 5.36.Случайная величина X имеет закон распределения, определяемый таблицей
| xk | 0,1 | 0,2 | 0,3 | 0,4 |
| pk | 0,2 | 0,4 | 0,3 | 0,1 |
Найти закон распределения случайной величины Y = 5Х — 1.
А 5.37.Пусть X – сумма очков при двух бросаниях игральной кости. Найти ее математическое ожидание и дисперсию.
А 5.38.Случайная величина X принимает значения х1 и х2 с
вероятностями 0,2 и 0,8 соответственно. Известны ее математическое ожидание М(Х) = 1,3 и дисперсия D(Х) = 0,16. Найти значения случайной величины Х.
А 5.39.В магазине имеются 10 телевизоров, из которых 4 дефектные. Пусть X – число исправных телевизоров среди трех выбранных. Найти закон распределения X, М(Х) и D(Х).
А 5.40.В магазин поступила обувь с двух фабрик в соотношении 2:3. Куплено 4 пары обуви. Найти закон распределения числа купленных пар обуви, изготовленных первой фабрикой. Найти
математическое ожидание, дисперсию и среднее квадратическое отклонение этой величины.
В 5.1.Два стрелка делают по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,5, вторым – 0,4. Составить закон распределения числа попаданий в мишень.
В 5.2.Вероятность попадания в цель при одном выстреле из орудия равна 0,4. Производится шесть выстрелов. Составить закон распределения числа: а) попаданий; б) непопаданий в цель.
В 5.3.Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые посетит студент, если в городе четыре библиотеки.
В 5.4.Обрыв связи произошел на одном из пяти звеньев телефонного кабеля. Монтер последовательно проверяет звенья для обнаружения места обрыва. Составить закон распределения количества обследованных звеньев, если вероятность обрыва связи одинакова для всех звеньев.
В 5.5.Вероятность того, что денежный автомат при опускании монеты сработает правильно, равна 0,97. Составить закон распределения числа опусканий монет в автомат до первого правильного срабатывания автомата.
В 5.6.Имеется пять различных ключей, из которых только один подходит к замку. Составить закон распределения числа опробований при открывании замка, если испробованный ключ в последующих попытках открыть замок: а) не участвует; б) участвует.
В 5.7.Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. Вычислить математическое ожидание и дисперсию этой случайной величины.
В 5.8.В лотерее на 100 билетов разыгрываются две вещи, стоимость которых 210 и 60 грн. Составить закон распределения суммы выигрыша для лица, имеющего: а) один билет; б) два билета. Стоимость билета 3 грн. Убедиться в справедливости свойства математического ожидания для суммы зависимых случайных величин.
В 5.9.Составить закон распределения случайной величины, выражающей число попаданий в мишень при четырех выстрелах, если вероятность попадания при каждом выстреле равна 0,3. Вычислить ее математическое ожидание и дисперсию, пользуясь только их определениями, а результаты проверить по формулам этих характеристик для случайной величины, распределенной по биномиальному закону.
В 5.10.На двух автоматических станках производятся одинаковые изделия. Известны законы распределения числа бракованных изделий, производимых в течение смены на каждом из станков:
а) для первого станка:
| Количество бракованных изделий | ||||
| Вероятность | 0,1 | 0,6 | 0,2 | 0,1 |
б) для второго станка:
| Количество бракованных изделий | |||
| Вероятность | 0,5 | 0,3 | 0,2 |
Составить закон распределения числа бракованных изделий, производимых в течение смены двумя станками вместе. На этом примере проверить выполнение свойств математических ожиданий и дисперсий: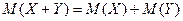 
.
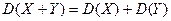
В 5.11.Дан закон распределения случайной величины Х:
| Значение | – 2 | |||
| Вероятность | 0,1 | 0,5 | 0,3 | 0,1 |
Составить законы распределения случайных величин Х 2 и 3Х.
В 5.12.Два баскетболиста по очереди забрасывают мяч в корзину с вероятностью попадания при каждом броске для первого 0,8, для второго – 0,7. Всего производится пять бросков. Составить законы распределения числа попаданий для каждого игрока, если начинает бросать первый баскетболист, а также закон распределения общего числа попаданий.
В 5.13.Даны законы распределения двух независимых случайных величин:
| Значение (Х) | Значение (Y) | |||||||
| Вероятность | 0,4 | 0,2 | 0,1 | 0,3 | Вероятность | 0,5 | 0,25 | 0,25 |
Составить закон распределения их разности, а затем проверить выполнение следующих свойств математических ожиданий и дисперсий: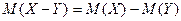 
; 
.
В 5.14.Даны законы распределения двух независимых случайных величин:
| Значение (Х) | – 4 | Значение (Y) | ||||
| Вероятность | 0,25 | 0,5 | 0,25 | Вероятность | 0,5 | 0,5 |
Составить закон распределения их средней арифметической.
В 5.15.Даны законы распределения двух независимых случайных величин
| Значение (Х) | -1 | Значение (Y) | |||||
| Вероятность | 0,2 | 0,3 | 0,5 | Вероятность | 0,1 | 0,3 | 0,6 |
Составить закон распределения их произведения. Проверить
выполнение следующего свойства математических ожиданий: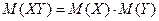 
.
Функция распределения случайной величины Х выражает
вероятность того, что Х примет значение, меньше х:
.
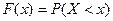
Свойства функции распределения: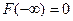 
, 
, 
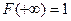
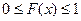
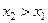
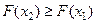
; если 
, то 
.
Вероятность попадания случайной величины Х в промежуток [a, b] определяется формулой
.
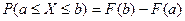
Если функция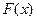 
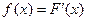
непрерывна и имеет всюду (кроме, возможно, конечного числа точек) непрерывную производную, то случайную величину Х называют непрерывной, а функцию 
называют плотностью вероятностей случайной величины X.
Имеют место формулы:
, 
, 
, 
.
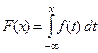
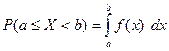
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник