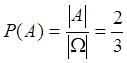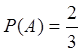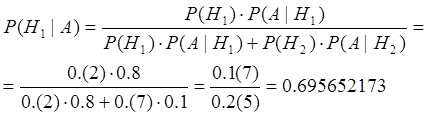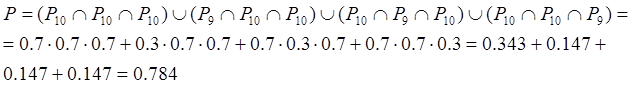Депо производит ремонт вагонов вероятность того что ремонт будет произведен со сдачей

Расчет вероятности выхода пассажиров из лифта на одном этаже. Определение вероятности того, что участок АС поезд пройдет без остановки

Страницы работы

Фрагмент текста работы

Пространство элементарных исходов в этом случае будет состоять из трёх равновероятных исходов:

, где

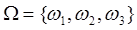
Интересующему нас событию. А благоприятны два элементарных исхода, т. е. .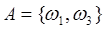

Применим классический метод вычисления вероятностей. Исходя из него вероятность возникновения события А равна

Ответ:

На участке АВ движения поезда имеется 12 светофоров. Вероятность остановки перед каждым из них равна 0.1. Вероятность того, что от пункта В до конечного пункта С поезд пройдет без остановки, равна 0.7. Определить вероятность того, что участок АС поезд пройдет без остановки.

Рассмотрим вероятность того, что поезд не остановится перед любым светофором, она равна Р_i = 1-0.1 = 0.9. Поскольку чтобы пройти участок АВ без остановки поезд не должен остановится не перед одним светофором, то вероятность того, что поезд не остановится на участке АВ, равна .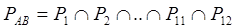

Исходя из сказанного, делаем вывод, что вероятность того, что поезд не остановится на участке АС, равна 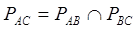, где Р_ВС есть вероятность прохода поездом участка ВС без остановки.

Рассчитаем перечисленные вероятности:

Р_АВ = 0.9*0.9*..*0.9 = 0.9 12 = 0.282429536

= 0.282429536*0.7 = 0.1977

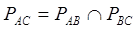
Игра между А и В ведётся на следующих условиях: в результате первого хода, который всегда делает А, он может выиграть с вероятностью 0.3. Если первым ходом А не выигрывает, то ход делает В и может выиграть с вероятностью 0.5. Если в этом ходу В не выиграет, то А делает второй ход, который может привести к выигрышу с вероятностью 0.4. Определить вероятность выигрыша В.

Поскольку вероятность выигрыша А на первом ходу равна 0.3, то вероятность того, что А не выиграет равна P_!A = 1-0.3 = 0.7. Отсюда можем сделать вывод, что В выиграет с вероятностью равной произведению вероятности того что не выиграет А и заданной в условии вероятности выигрыша В при условии что А не выиграл на первом ходу.

Значит:

В тире имеется девять ружей, из которых пристрелянными являются только два. Вероятность попадания в цель из пристрелянного ружья равна 0.8, а из не пристрелянного – 0.1. Выстрелом из одного наугад взятого ружья мишень поражена. Определить вероятность того, что взято пристрелянное ружьё.

В результате проведения вероятностного эксперимента было выяснено что событие А = <выстрелом из выбранного наугад ружья цель поражена>выполнилось. В связи с этим можно выдвинуть две гипотезы:

Исходя из сделанных предположений, по формуле Байерса, можем найти вероятность того, что было выбрано пристрелянное ружьё. Для того чтобы применить формулу Байерся произведём следующие расчеты:

Исходя из условия Р(H₁) = 2/9 = 0.(2), Р(H₂) = 7/9 = 0.(7), Р(А| H₁) = 0.8,

Применим формулу Байерса:

Ответ: P(H1|A) = 0.695652173

Вероятность попадания стрелком в десятку равно 0.7, а в девятку – 0.3. Определить вероятность того, что данный стрелок при трех выстрелах наберёт не менее 29 очков.

Рассмотрим данный эксперимент. Стрелок наберёт 29 или 30 очков только в следующих случаях:

1) Если он поразит десятку со всех трёх выстрелов.

2) Если с двух выстрелов он поразит десятку, а с одного – девятку, причем делать он это может в любом порядке.

Отсюда вытекает, что вариантов набора может быть всего четыре. Поэтому вероятность мы можем рассчитать по формуле:

,

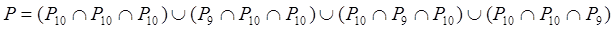
где Р₁₀ = 0.7 – вероятность поразить десятку, Р₉ = 0.3 – вероятность поразить девятку. Подставив в данную формулу заданные значения вероятностей, получим Р – искомую вероятность.

Депо производит ремонт вагонов. Вероятность того, что ремонт будет произведён со сдачей с первого предъявления, равна 0.8. Найти вероятность того, что из ста вагонов, отремонтированных в депо:

а) ровно 50 вагонов будут сданы с первого предъявления;

б) от 40 до 80 вагонов будут сданы с первого предъявления;

По условию задачи проводятся n = 100 независимых испытаний, проверяется качество ремонта, и вероятность появления «успеха» ( ремонт произведён со сдачей с первого предъявления) в каждом испытании Р = 0.8; соответственно вероятность «неудачи» Q = 1-P = 1-0.8 = 0.2. Для нахождения искомой вероятности события

Источник

Диаграммы Венна-Эйлера, Формула Байеса, Формула Бернулли, Формула Муавра-Лапласа — файл ТВиМС_ргр1_вар_24.doc

Доступные файлы (12):

ТВиМС_ргр1_вар_01.doc	325kb.	16.10.2008 10:30	скачать
ТВиМС_ргр1_вар_05.doc	272kb.	06.12.2008 13:36	скачать
ТВиМС_ргр1_вар_06.doc	185kb.	06.12.2008 13:35	скачать
ТВиМС_ргр1_вар_08.doc	438kb.	16.10.2008 10:40	скачать
ТВиМС_ргр1_вар_09.doc	256kb.	16.10.2008 10:40	скачать
ТВиМС_ргр1_вар_10.doc	85kb.	06.12.2008 13:36	скачать
ТВиМС_ргр1_вар_13.doc	246kb.	16.10.2008 10:40	скачать
ТВиМС_ргр1_вар_14.doc	237kb.	16.10.2008 10:40	скачать
ТВиМС_ргр1_вар_17.doc	324kb.	16.10.2008 10:39	скачать
ТВиМС_ргр1_вар_20.doc	110kb.	16.10.2008 10:39	скачать
ТВиМС_ргр1_вар_22.doc	128kb.	06.12.2008 13:35	скачать
ТВиМС_ргр1_вар_24.doc	335kb.	16.10.2008 10:39	скачать

ТВиМС_ргр1_вар_24.doc

Белорусский Государственный Университет Транспорта

Кафедра “ Прикладная математика и теория надежности“

Расчетно – графическая

работа №1 (вариант 24)
Выполнил Проверил

студент гр. преподаватель

Задание №1.
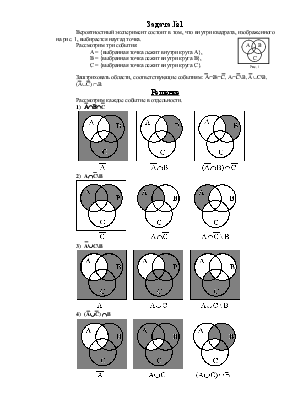
Вероятностный эксперимент состоит в том, что внутри квадрата выбирается наугад точка. Рассмотрим три события :

Заштриховать области, соответствующие событиям :

ABC

Задание №2
Первенство по баскетболу разыгрывают 18 команд, среди которых 2 команды экстракласса. Для уменьшения общего числа игр команды путем жеребьевки разбиваются на две группы. Какова вероятность того, что две команды экстракласса окажутся в разных подгруппах.
Решение :
Рассмотрим событие:

Число всех возможных исходов (т.е. событий пространства Ω):

N(Ω)= 153;

Число элементарных исходов, благоприятствующих событию А:

N(A)=

Согласно классическому определению вероятности;

P(A) = N(A)/N(Ω)=81/153=0.53
Ответ : P(A) = 0.53.

Задание №3

На плоскости проведены параллельные линии, расстояния между которыми попеременно равны 1.5 и 8. Определить вероятность того, что наугад брошенный на эту плоскость круг радиуса 2.5 см не будет пересечен ни одной линией.
Решение :

Решим задачу геометрическим методом.

Интересующее нас событие :

Вероятность события А равна отношению длины отрезка, при нахождении в пределах которой шар не пересекается линиями (CD), к длине отрезка АВ :

Ответ : P(A) = 0.316

Задание №4

Работа прибора прекратилась вследствие выхода из строя одной лампы из общего числа 17. Отыскание этой лампы производится путем поочередной замены каждой лампы новой. Определить вероятность того, что придется проверить 10 ламп, если вероятность выхода из строя каждой лампы равна 0,2.

Решение :
Рассмотрим события :

Н_i=

Ответ : Р(А) = 0.027

У остановочной платформы на привокзальной площади останавливаются автобусы 8 маршрутов с одинаковой частотой движения. Определить вероятность того, что из двух первых автобусов один окажется нужного маршрута.

B_i=

P(A) = P(B₁) + P()∙P(B₂)=

Ответ : P(A) = 0.234

Задача №6

Для контроля продукции из трех партий деталей взята для испытания одна. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в других – все доброкачественные ?
Решение :

Найдем искомую вероятность по формуле полной вероятности :

P(A) = P(H)∙P(A|H) =

Ответ : P(A) = 0.222

Задание №7
Для сигнализации о том, что режим работы автоматической линии станков отклоняется от нормального, используется индикатор, принадлежащий с вероятностями 0.2; 0.3 и 0.5 к одному из трех типов, для которых вероятности срабатывания при нарушении нормальной работы линии равны соответственно 1; 0.75; 0.4. От индикатора получен сигнал. Какова вероятность того, что сработал индикатор второго типа ?
Решение :
Рассмотрим событие :

Н_i= <индикатор i-го типа>

Ответ : P(H₂|A) = 0.36

Задание №8
Вероятность того, что лампа останется исправной после 1000 часов работы, равна 0.2. Какова вероятность того, что хотя бы одна из трех ламп останется исправной после 1000 часов работы ?
Решение :
Рассмотрим события :

В_i =

P(A) = 1 – P() = 1 – =0.488
Ответ : Р(А) = 0.488

Задание №9.
Депо производит ремонт вагонов. Вероятность того, что ремонт будет произведен со сдачей с первого предъявления, равна 0.75. Найти вероятность того, что из 100 вагонов, отремонтированных в депо:

а) ровно 60 вагонов будут сданы с первого предъявления;

б) от 40 до 70 вагонов будут сданы с первого предъявления.
Решение:
а) по условию задачи проводится n=100 независимых испытаний (проверка качества ремонта) и вероятность появления “успеха” (ремонт произведен со сдачей с первого предъявления) в каждом испытании p = 0.75; соответственно вероятность “неудачи” q = 1-‍‍p = 0.25

Для нахождения искомой вероятности события

воспользуемся локальной теоремой Муавра-Лапласа:

Следовательно, вероятность интересующего нас события Р(А)=Р₁₀₀(60)≈2,3∙10 -4

Источник