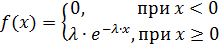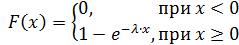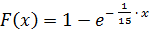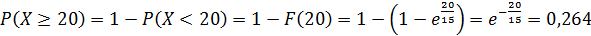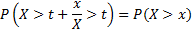Экспоненциально распределенная случайная величина
На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ — распределенных по показательному (или экспоненциальному) закону.
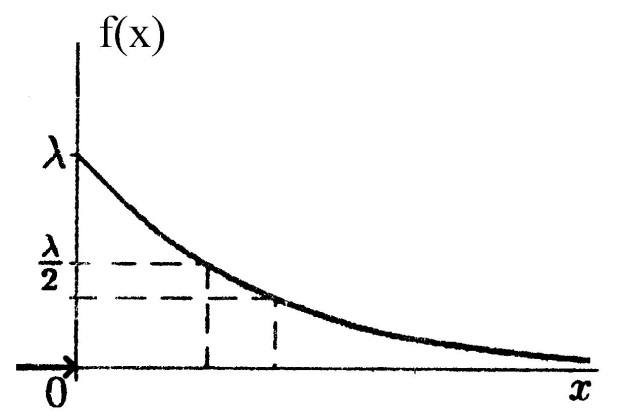
Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:
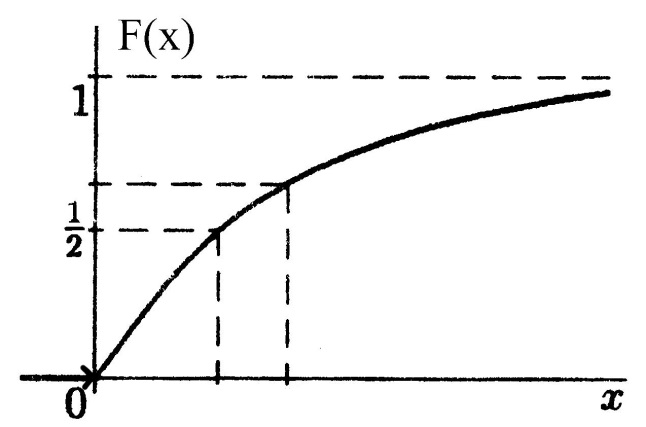
Функция распределения величины $X$:
Здесь $\lambda$ — единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/\lambda$, $D(X)=1/\lambda^2$.
Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $\lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.
В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.
Примеры решений
Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.
Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?
Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $\lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.
Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^<-2t>$ при $t\ge 0$ и $f(t)=0$ при $t\lt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.
Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.
Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^<-3x>$ при $x \gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача 8. Непрерывная случайная величина $\xi$ распределена по показательному закону с параметром $\lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $\xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $\xi$ и вероятность того, что $\xi$ принимает значения, меньшие своего математического ожидания.
Задача 9. Случайная величина $\xi$ распределена по показательному закону с параметром 2. Найти $M_<\xi>$, $D_<\xi>$ вероятность попадания $\xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $\xi$.
Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(\lambda)$. Найдите вероятность события $|Х — МХ | \lt 3\sigma$ («правило $3\sigma$» для показательного распределения).
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Источник
Показательный (экспоненциальный закон распределения).
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
Функция распределения имеет вид:
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
, 
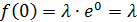
То есть при 
Пример.
Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется не менее 20дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.
Решение:
По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:
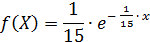
Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть
но проще это сделать, используя функцию распределения:
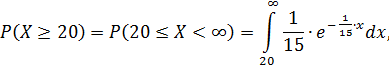
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.
Источник
Показательный (экспоненциальный закон распределения)
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
Функция распределения имеет вид:
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
То есть при 
Пример.
Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.
Решение:
По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:
Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть
но проще это сделать, используя функцию распределения:
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.
Равномерный закон распределения.
Непрерывная случайная величина Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, то есть
Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.
Дисперсия имеет вид:
Найдем вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал 
, принадлежащий целиком отрезку [a, b]:
Функция распределения примет вид:
Пример.
Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты.
Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.
Решение:
Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0;2] имеет равномерный закон распределения f (x)=1/2.
Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 1/4 от равной единице площади прямоугольника, т.е.
Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение:
Источник
Законы распределения времени безотказной работы
При изучении надежности технических устройств наиболее часто применяются следующие законы: экспоненциальный, нормальный, Релея, Вейбулла-Гнеденко.
Рассмотрим наиболее часто используемые в теории надежности семейства распределения случайной величины – параметрические, т. е. зависящие от одного или нескольких параметров. Функция
задает экспоненциальное (или показательное) распределение. Экспоненциальным законом распределения можно аппроксимировать время безотказной работы большого числа элементов. Это относится к элементам радиоэлектронной аппаратуры и машинам, эксплуатируемым в период после окончания приработки и до существенного проявления постепенных отказов. Экспоненциальное распределение применяется в областях, связанных с «временем жизни»: в медицине – продолжительность жизни больных, в надежности – продолжительность безотказной работы устройств, в психологии – время, затраченное на выполнение тестовых задач.
Это распределение имеет один параметр 
, где T1 – средняя наработка элемента до отказа. Таким образом, параметр λ характеризует число отказов элемента в единицу времени и называется интенсивность отказов. Плотность экспоненциального распределения задается как:
(9.1)
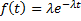
Функция надежности определяет вероятность безотказной работы за время t по следующей формуле:
(9.2)
Интенсивность отказов в данном случае есть величина постоянная.
Экспоненциальное распределение выделяется среди других распределений свойством «отсутствия памяти». Пусть Х – время службы некоторого изделия с экспоненциальным законом распределения. «Отсутствие памяти» означает, что изделие, проработавшее время t, имеет такое же распределение, что и новое, только что начавшее работу. Математически это свойство выражается в виде следующего равенства:
для любых t, x ≥ 0. Данное свойство как бы исключает износ и старение изделия.
Числовые характеристики экспоненциального распределения выражается через его параметр: математическое ожидание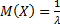 
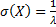
, дисперсия 
, среднее квадратическое отклонение 
.
Для характеристики постепенных отказов обычно используют другие законы распределения.
Нормальному закону распределения (распределению Гаусса) подчиняются:
— время безотказной работы производственных систем, потеря работоспособности которых связана в основном с постепенными отказами, при этом доля внезапных отказов весьма мала;
— случайные величины массовых явлений, на которые оказывает влияние большое количество различных по величине факторов (например, износ и усталость деталей, технологические погрешности, точность размеров, получаемых при обработке и т. д.).
Нормальному закону распределения подчиняются только непрерывные случайные величины. Поэтому нормальное распределение может быть задано:
, –∞
— вероятность безотказной работы
(9.6)
(9.7)
(9.8)
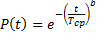
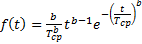
— среднее время безотказной работы
, (9.9)
Следует отметить, что при b = 1 распределение Вейбулла-Гнеденко превращается в экспоненциальное, а при b = 2 – в распределение Релея, при b = 3.3 распределение близко к нормальному. Оно хорошо описывает наработку деталей по усталостным нарушениям, наработку до отказа подшипников, а также используется для оценки надежности деталей и узлов машин, автомобилей.
Закон Релея может быть применен при исследовании надежности изделий, имеющих элементы с выраженным эффектом старения:
Если случайная величина распределена по закону Релея, то вероятность безотказной работы определяется из уравнения:
, (9.10)
где σ – среднеквадратическое отклонение (параметр распределения).
Частота отказов (плотность распределения) будет иметь вид:
. (9.11)
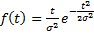
Интенсивность отказов находится так:
. (9.12)
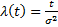
Средняя наработка на отказ (средний ресурс, средний срок службы, среднее время восстановления работоспособного состояния) определяется следующим уравнением:
. (9.13)
Следует также отметить, что существуют и другие законы распределения времени до отказа, однако применяются они достаточно редко и рассматриваться нами не будут.
Источник