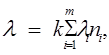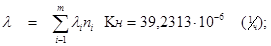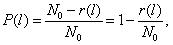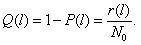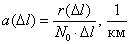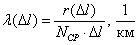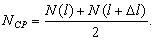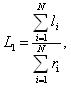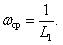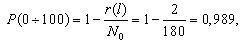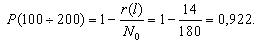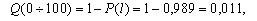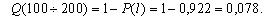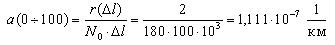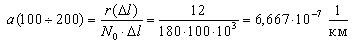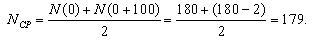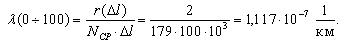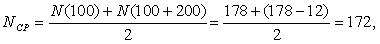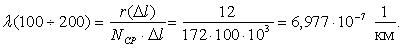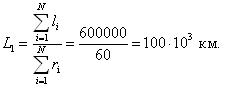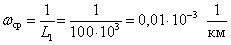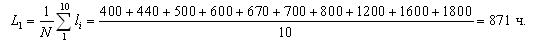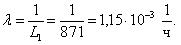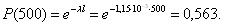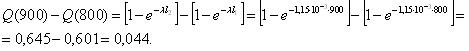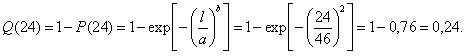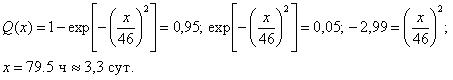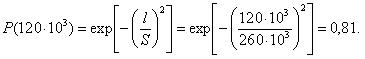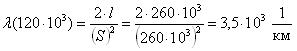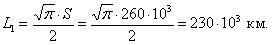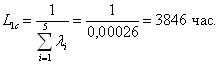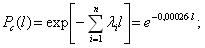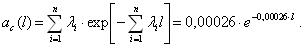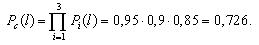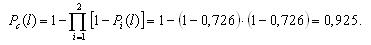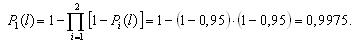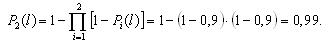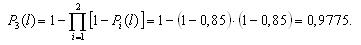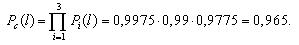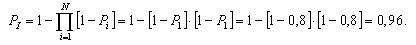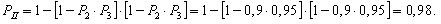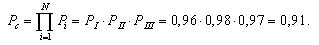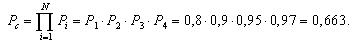Интенсивность отказов после ремонта
Она обозначается буквой λ (лямбда):
λ — интенсивность отказов после ремонта (за месяц в %);
n – число автотранспорта, вышедших из строя (за месяц в шт.);
N – общее число отремонтированного автотранспорта (за месяц в шт.).
Нормативные значения данных прописаны в п. 3.7 карты процесса. Они составлялись на основе значений, которые были получены в течении года при анализе этого процесса. Таким образом, был получен результат, который оказался приемлемым для данной характеристики.
Итак, нормативные значения:
Подставляя значение в формулу, получим:
При нормативных значениях n=10 и N=40, интенсивность отказов после ремонта будет равна25% — целью для рассматриваемого критерия будет условие: λ≤25%
Для составления диаграммы возьмем расчетный период – 1 год.
Табл.5. Данные по уровню интенсивности отказов за год
| Месяц | Число автотранспорта, вышедших из строя (за месяц в шт) | Интенсивность отказов после ремонта (за месяц в %) |
| Январь | ||
| Февраль | ||
| Март | ||
| Апрель | ||
| Май | 7,5 | |
| Июнь | ||
| Июль | 12,5 | |
| Август | ||
| Сентябрь | 17,5 | |
| Октябрь | 7,5 | |
| Ноябрь | ||
| Декабрь |
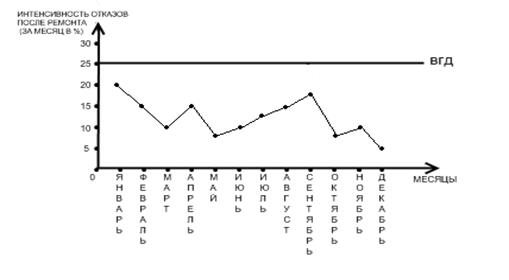
Рис. 1. Диаграмма для показателя «Интенсивность отказов»
Проанализируем процесс, используя признаки, указывающие на неуправляемое состояние процесса.
Выводы по диаграмме:
· Ни одна из точек не выходит за границу допуска;
· мы наблюдаем положительный тренд (тенденция на увеличение уровня интенсивности отказов);
· точки не приближаются к контрольным пределам;
· необходимо проведение плана предупреждающих действий.
Рассмотрим возрастающий тренд: он имеет протяженность – 5 точек, с мая по сентябрь. С чем это связано будет рассмотрено в диаграмме Исикавы, план предупреждающих действий будет разработан ниже.
Источник
РАСЧЕТ ОСНОВНЫХ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
На стадии прикидочного и ориентировочного расчетов электротехнических устройств рассчитывают основные показатели надежности.
Основными качественными показателями надежности является:
— вероятность безотказной работы;
— средняя наработка до отказа.
Интенсивность отказов l(t) — это число отказавшихn(t) элементов устройства в единицу времени, отнесенное к среднему общему числу элементов N(t), работоспособных к моменту времени Δt[ 9]
где Δt — заданный отрезок времени.
Например: 1000 элементов устройства работали 500 часов. За это время отказали 2 элемента. Отсюда,
l (t)=n(t)/(Nt*Δt)=2/(1000*500)=4*10 -6 1/ч, то есть за 1 час может отказать 4-е элемента из миллиона.
Показатели интенсивности отказов l(t) элементов являются справочными данными, в приложении Г приводятся интенсивности отказов l(t)для элементов, часто применяемых в схемах.
Электротехническое устройство состоит из большого числа комплектующих элементов, поэтому определяют эксплуатационную интенсивность отказов l(t) всего устройства как сумму интенсивностей отказов всех элементов, по формуле [ 11]
где k – поправочный коэффициент, учитывающий относительное изменение средней интенсивности отказов элементов в зависимости от назначения устройства;
m – общее количество групп элементов;
nі — количество элементов в і- й группе с одинаковой интенсивностью отказов lі(t) .
Вероятность безотказной работы P(t) представляет собой вероятность того, что в пределах указанного периода времени t, отказ устройства не возникнет. Этот показатель определяется отношение числа устройств, безотказно проработавших до момента времени t к общему числу устройств, работоспособных в начальный момент.
Например, вероятность безотказной работы P(t) =0,9 представляет собой вероятность того, что в пределах указанного периода времени t= 500час, отказ произойдет в (10-9=1) одном устройстве из десяти, и из 10 устройств 9 будут работать без отказов.
Вероятность безотказной работы P(t) =0,8 представляет собой вероятность того, что в пределах указанного периода времени t=1000час, отказ произойдет двух 2 устройствах из ста, и из 100 устройств 80 устройств будут работать без отказов.
Вероятность безотказной работы P(t) =0,975 представляет собой вероятность того, что в пределах указанного периода времени t=2500час, отказ произойдет в 1000-975=25 устройствах из тысячи, а 975 устройств будут работать без отказов.
Количественно надёжность устройства оценивается как вероятность P(t) события, заключающегося в том, что устройство в течение времени от 0 до t будет безотказно выполнять свои функции. Величина P(t) вероятность безотказной (рассчитанное значение Р(t) не должно быть менее 0,85) работы определяется выражением
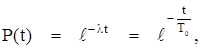
где t – время работы системы, ч (t выбирается из ряда: 1000, 2000, 4000, 8000, 10000 ч.);
λ – интенсивность отказов устройства, 1 /ч;
Т0 – наработка на отказ, ч.
Расчёт надёжности заключается в нахождении общей интенсивности отказов λ устройства и наработки на отказ:
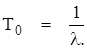
Время восстановления устройства при отказе включает в себя время поиска неисправного элемента, время его замены или ремонта и время проверки работоспособности устройства.
Среднее время восстановления Тв электротехнических устройств может выбираться из ряда 1, 2, 4, 6, 8, 10, 12, 18, 24, 36, 48 час. Меньшие значения соответствуют устройствам с высокой ремонтнотпригодностью. Среднее время восстановления Тв можно уменьшить используя встроенный контроль или самодиагностику, модульное исполнение составных частей, доступный монтаж.
Значение коэффициента готовности 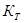
где Т0 – наработка на отказ, ч.
Тв – среднее время восстановления, ч.
Надёжность элементов в значительной степени зависит от их электрических и температурных режимов работы. Для повышения надёжности элементы необходимо использовать в облегченных режимах, определяемых коэффициентами нагрузки.
Коэффициент нагрузки – это отношение расчетного параметра элемента в рабочем режиме к его максимально допустимому значению. Коэффициенты нагрузки различных элементов могут сильно отличаться.
При расчёте надежности устройства все элементы системы разбиваются на группы элементов одного типа и одинаковыми коэффициентами нагрузки Кн.
Интенсивность отказа і- го элемента определяется по формуле
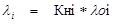
где Кн і — коэффициент нагрузки, рассчитывают в картах рабочих режимов, либо задают полагая, что элемент работает в нормальных режимах, в приложении Г приводятся значения коэффициентов нагрузки элементов;
λ 0і – базовая интенсивность отказов і — го элемента приводится в приложении Г.
Часто, для расчета надежности, используются данные интенсивности отказа λ 0і аналогов элементов.
Пример расчета надежности устройства состоящего из покупного комплекса BT-85W импортного производства и разрабатываемого на элементной базе серийного производства источника питания.
Интенсивности отказов изделий импортного производства определяют, как обратную величину времени эксплуатации, (иногда берут гарантийный срок обслуживания изделия) из расчета эксплуатации в одни сутки определенного числа часов.
Гарантийный срок службы покупного импортного изделия 5 лет, изделие будет работать 14,24часа в сутки:
Т=14,24час х 365дней х 5 лет = 25981 часов – время наработки на отказ.

Расчёты и исходные данные выполняют на ЭВМ с использованием программ Excel и приводятся в таблицах 10.1 и 10.2. Пример расчета приводится в таблице 10.1.
Таблица 10.1 – Расчет надежности системы
| Наименование и тип элемента или аналога | Коэффи-циент, нагрузки, Кнi | ||||
| λi *10 -6 , 1 /ч | λi *Кнi*10 -6 1 /ч | Кол-во ni, | nі *λi *10 -6 , 1 /ч | ||
| Комплекс BT-85W | 1,00 | 38,4897 | 38,4897 | 38,4897 | |
| Конденсатор К53 | 0,60 | 0,0200 | 0,0120 | 0,0960 | |
| Розетка (вилка)СНП268 | 0,60 | 0,0500 | 0,0300 | 0,0900 | |
| Микросхема TRS | 0,50 | 0,0460 | 0,0230 | 0,0230 | |
| Резистор ОМЛТ | 0,60 | 0,0200 | 0,0120 | 0,0120 | |
| Вставка плавкая ВП1-1 | 0,30 | 0,1040 | 0,0312 | 0,0312 | |
| Стабилитрон 12В | 0,50 | 0,4050 | 0,2500 | 0,4050 | |
| Индикатор 3Л341Г | 0,20 | 0,3375 | 0,0675 | 0,0675 | |
| Кнопочный выключатель | 0,30 | 0,0100 | 0, 0030 | 0,0030 | |
| Фотодиод | 0,50 | 0,0172 | 0,0086 | 0,0086 | |
| Соединение сваркой | 0,40 | 0,0001 | 0,0004 | 0,0004 | |
| Провод, м | 0,20 | 0,0100 | 0,0020 | 0,2 | 0,0004 |
| Соединение пайкой | 0,50 | 0,0030 | 0,0015 | 0,0045 | |
| l всего устройства | å=39,2313 |
Определяем общую интенсивность отказов устройства
Тогда наработка на отказ согласно выражению (10.2) и соответственно равна
Для определения вероятности безотказной работы за определенный промежуток времени построим график зависимости:
Таблица 10.2 — Расчет вероятности безотказной работы
| t(час) | |||||||||
| P(t) | 0,97 | 0,9 | 0,8 | 0,55 | 0,74 | 0,65 | 0,52 | 0,4 | 0,34 |
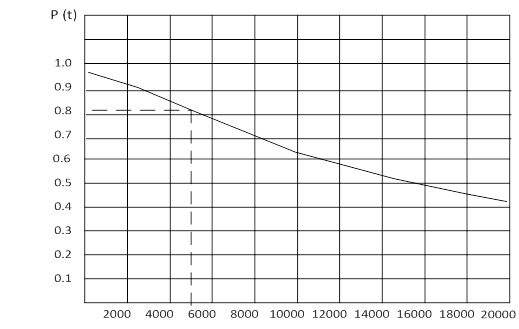
График зависимости вероятности безотказной работы от времени работы показан на рисунке 10.1.
Рисунок 10.1 – Вероятность безотказной работы от времени работы
Для устройства, как правило задают вероятность безотказной работы от 0,82 до 0,95. По графику рисунка 10.1 можем определить для разработанного устройства при заданной вероятности безотказной работы Р(t)=0,82, время наработки на отказ То=5000час.
Расчет выполнен для случая, когда отказ любого элемента приводит к отказу всей системы в целом, такое соединение элементов называется логически последовательным или основным. Надежность можно повысить резервированием.
Например. Технология элементов обеспечивает среднюю интенсивность отказов элементарных деталей li=1*10 -5 1/ч. При использовании в устройстве N=1*10 4 элементарных деталей суммарная интенсивность отказов lо= N*li=10 -1 1/ч. Тогда среднее время безотказной работы устройства To=1/lо=10 ч. Если выполнить устройство на основе 4-х параллельно включенных одинаковых устройств, то среднее время безотказной работы увеличится в N/4=2500 раз и составит 25000 ч. или 34 месяца или около 3 лет.
Формулы позволяют выполнить расчет надежности устройства, если известны исходные данные — состав устройства, режим и условия его работы, интенсивности отказов его элементов.
Источник
—>ДИАГНОСТИКА И НАДЕЖНОСТЬ —>
1.1 Вероятность безотказной работы
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):
где N0 – число элементов в начале испытания; r ( l ) – число отказов элементов к моменту наработки. Следует отметить, что чем больше величина N 0 , тем с большей точностью можно рассчитать вероятность P ( l).
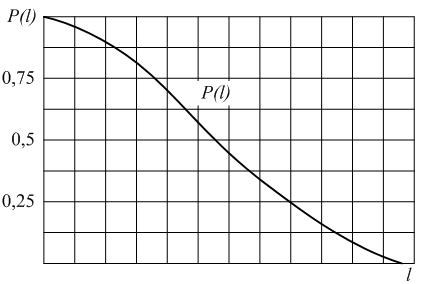
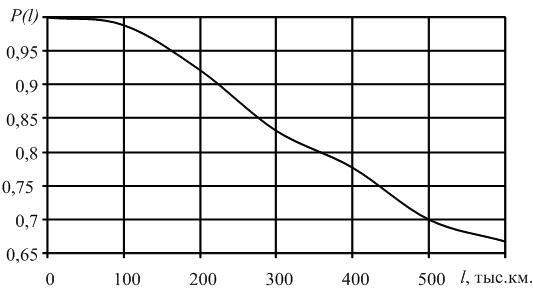
В начале эксплуатации исправного локомотива P(0) = 1, так как при пробеге l = 0 вероятность того, что ни один элемент не откажет, принимает максимальное значение – 1. С ростом пробега l вероятность P(l) будет уменьшаться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность безотказной работы будет стремиться к нулю P(l→∞) = 0. Таким образом в процессе наработки величина вероятности безотказной работы изменяется в пределах от 1 до 0. Характер изменения вероятности безотказной работы в функции пробега показан на рис. 1.1.
Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки
Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P ( l ), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.
1.2 Вероятность отказа
Вероятностью отказа называют вероятность того, что при определенных условиях эксплуат ации, в предела х заданной наработки произойдет хотя бы один отказ.
Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):
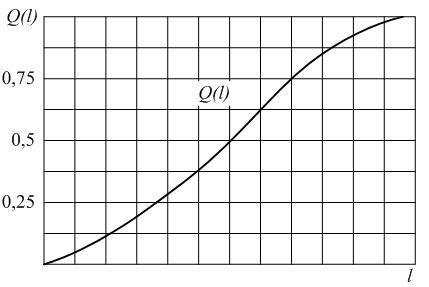
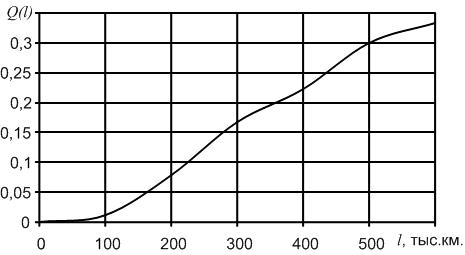
В начале эксплуатации исправного локомотива Q (0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q ( l ) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q ( l →∞ ) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2. Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.
Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки
1.3 Частота отказов
Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы.
Частота отказов обозначается как 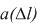
где – 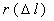
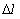
Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей.
Характер изменения частоты отказов в функции пробега показан на рис. 1.3.
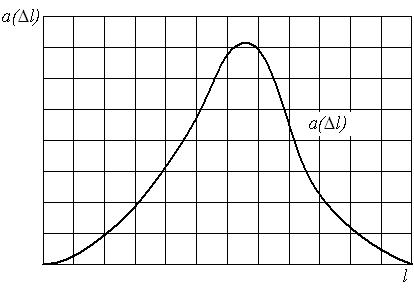
Рис. 1.3. График изменения частоты отказов в зависимости от наработки
1.4 Интенсивность отказов
Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Интенсивность отказов обозначается как 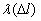
где
Как правило, интенсивность отказов 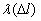
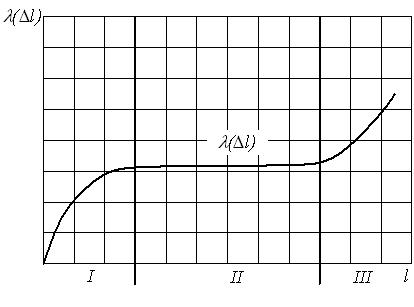
На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега.
Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки
На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс экс-плуатации элемента или объекта в целом.
Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера.
Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента.
Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной.
1.5 Средняя наработка до отказа
Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа.
Средняя наработка до отказа обозначается как L1 и определяется по формуле (1.5):
где li – наработка до отказа элемента; ri – число отказов.
Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента.
1.6 Среднее значение параметра потока отказов
Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени.
Среднее значение параметра потока отказов обозначается как W ср и определяется по формуле (1.6):
1.7 Пример расчета показателей безотказности
Исходные данные.
В течение пробега от 0 до 600 тыс. км., в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N 0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6.
Требуется.
Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени.
Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1.
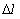 , тыс. км , тыс. км | 0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
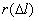 | 2 | 12 | 16 | 10 | 14 | 6 |
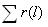 | 2 | 14 | 30 | 40 | 54 | 60 |
Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:
Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.
Произведем расчет частоты отказов по уравнению (1.3).
Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки.
Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:
Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:
Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.
По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.
Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.).
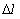 , тыс.км. , тыс.км. | 0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
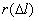 | 2 | 12 | 16 | 10 | 14 | 6 |
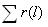 | 2 | 14 | 30 | 40 | 54 | 60 |
| P(l) | 0,989 | 0,922 | 0,833 | 0,778 | 0,7 | 0,667 |
| Q(l) | 0,011 | 0,078 | 0,167 | 0,222 | 0,3 | 0,333 |
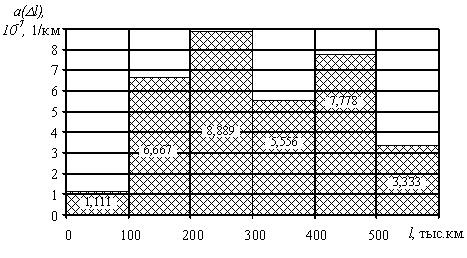
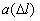 10 -7 , 1/км 10 -7 , 1/км | 1,111 | 6,667 | 8,889 | 5,556 | 7,778 | 3,333 |
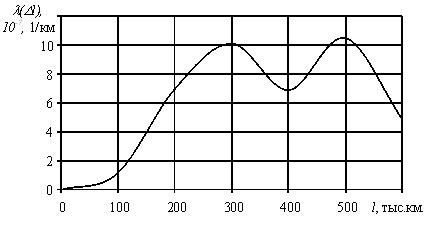
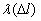 10 -7 , 1/км 10 -7 , 1/км | 1,117 | 6,977 | 10,127 | 6,897 | 10,526 | 4,878 |
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.
Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки
Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0.
Рис. 1.6. График изменения вероятности отказа в зависимости от наработки
Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).
Рис. 1.7. График изменения частоты отказов в зависимости от наработки
На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки.
Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки
2.1 Экспоненциальный закон распределения случайных величин
Экспоненциальный закон достаточно точно описывает надежность узлов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов показали его недостаточную приемлемость.
Исходные данные.
В результате испытания десяти топливных насосов высокого давления получены наработки их до отказа: 400, 440, 500, 600, 670, 700, 800, 1200, 1600, 1800 ч. Предполагая, что наработка до отказа топливных насосов подчиняется экспоненциальному закону распределения.
Требуется.
Оценить величину интенсивности отказов , а также рассчитать вероятность безотказной работы за первые 500 ч. и вероятность отказа в промежутке времени между 800 и 900 ч. работы дизеля.
Во-первых, определим величину средней наработки топливных насосов до отказа по уравнению:
Затем рассчитываем величину интенсивности отказов:
Величина вероятности безотказной работы топливных насосов при наработке 500 ч составит:
Вероятность отказа в промежутке между 800 и 900 ч. работы насосов составит:
2.2 Закон распределения Вэйбулла-Гнеденко
Закон распределения Вейбулла-Гнеденко получил широкое распространение и используется применительно к системам, состоящим из рядов элементов, соединенных последовательно с точки зрения обеспечения безотказности системы. Например, системы, обслуживающие дизель-генераторную установку: смазки, охлаждения, питания топливом, воздухом и т.д.
Исходные данные.
Время простоя тепловозов в неплановых ремонтах по вине вспомогательного оборудования подчиняется закону распределения Вейбулла-Гнеденко с параметрами b=2 и a=46.
Требуется.
Необходимо определить вероятность выхода тепловозов из неплановых ремонтов после 24 ч. простоя и время простоя, в течение которого работоспособность будет восстановлена с вероятностью 0,95.
Найдем вероятность восстановления работоспособности локомотива после простоя его в депо в течение суток по уравнению:
Для определения времени восстановления работоспособности локомотива с заданной величиной доверительной вероятности также используем выражение:
2.3 Закон распределения Рэлея
Закон распределения Рэлея используется в основном для анализа работы элементов, имеющих ярко выраженный эффект старения (элементы электрооборудования, различного рода уплотнения, шайбы, прокладки, изготовленные из резиновых или синтетических материалов).
Исходные данные.
Известно, что наработки контакторов до отказа по параметрам старения изоляции катушек можно описать функцией распределения Рэлея с параметром S = 260 тыс.км.
Требуется.
Для величины наработки 120 тыс.км. необходимо определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа катушки электромагнитного контактора.
3.1 Основное соединение элементов
Система, состоящая из нескольких независимых элементов, связанных функционально таким образом, что отказ любого из них вызывает отказ системы, отображается расчетной структурной схемой безотказной работы с последовательно соединенными событиями безотказной работы элементов.
Исходные данные.
Нерезервированная система состоит из 5 элементов. Интенсивности их отказов соответственно равны 0,00007; 0,00005; 0,00004; 0,00006; 0,00004 ч-1
Требуется.
Необходимо определить показатели надежности системы: интенсивность отказов, среднее время наработки до отказа, вероятность безотказной работы, частота отказов. Показатели надежности P(l) и a(l) получить в интервале от 0 до 1000 часов с шагом в 100 часов.
Вычислим интенсивность отказа и среднюю наработку до отказа по следующим уравнениям:
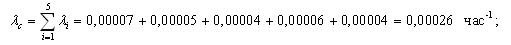
Значения вероятности безотказной работы и частоты отказов получим, используя уравнения приведенные к виду:
Результаты расчета P(l) и a(l) на интервале от 0 до 1000 часов работы представим в виде табл. 3.1.
| l, час | P(l) | a(l), час -1 |
| 0 | 1 | 0,00026 |
| 100 | 0,974355 | 0,000253 |
| 200 | 0,949329 | 0,000247 |
| 300 | 0,924964 | 0,00024 |
| 400 | 0,901225 | 0,000234 |
| 500 | 0,878095 | 0,000228 |
| 600 | 0,855559 | 0,000222 |
| 700 | 0,833601 | 0,000217 |
| 800 | 0,812207 | 0,000211 |
| 900 | 0,791362 | 0,000206 |
| 1000 | 0,771052 | 0,0002 |
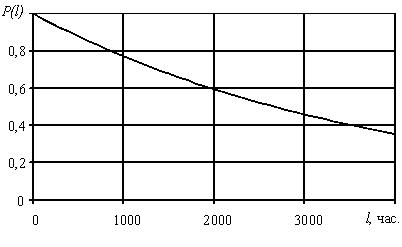
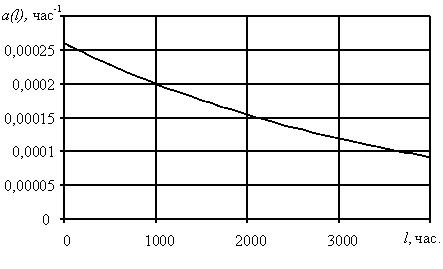
Графическая иллюстрация P(l) и a(l) на участке до средней наработки до отказа представлена на рис. 3.1, 3.2.
Рис. 3.1. Вероятность безотказной работы системы.
Рис. 3.2. Частота отказов системы.
3.2 Резервное соединение элементов
Исходные данные.
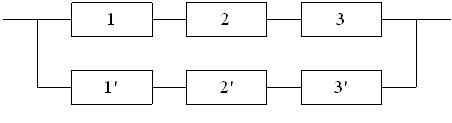
На рис. 3.3 и 3.4 показаны две структурные схемы соединения элементов: общего (рис. 3.3) и поэлементного резервирования (рис. 3.4). Вероятности безотказной работы элементов соответственно равны P1(l) = P ’1(l) = 0,95; P2(l) = P’2(l) = 0,9; P3(l) = P ’3(l) = 0,85.
Требуется.
Необходимо рассчитать надежность двух систем.
Рис. 3.3. Схема системы с общим резервированием.
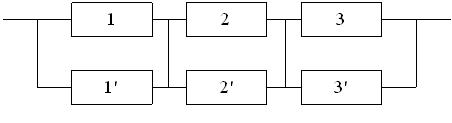
Рис. 3.4. Схема системы с поэлементным резервированием.
Вероятность безотказной работы блока из трех элементов без резервирования рассчитаем по выражению:
Вероятность безотказной работы той же системы при общем резервировании (рис. 3.3) составит:
Вероятности безотказной работы каждого из трех блоков при поэлементном резервировании (рис. 3.4) будут равны:
Вероятность безотказной работы системы при поэлементном резервировании составит:
Таким образом, поэлементное резервирование дает более существенное увеличение надежности (вероятность безотказной работы возросла с 0,925 до 0,965, т.е. на 4%).
Исходные данные.
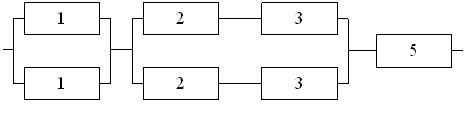
На рис. 3.5 представлена система с комбинированным соединением элементов. При этом вероятности безотказной работы элементов имеют следующие значения: P1=0,8; Р2=0,9; Р3=0,95; Р4=0,97.
Требуется.
Необходимо определить надежность системы. Также необходимо определить надежность этой же системы при условии, что резервные элементы отсутствуют.
Рис.3.5. Схема системы при комбинированном функционировании элементов.
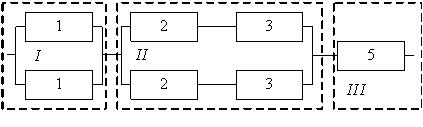
Для расчета в исходной системе необходимо выделить основные блоки. В представленной системе их три (рис. 3.6). Далее рассчитаем надежность каждого блока в отдельности, а затем найдем надежность всей системы.
Рис. 3.6. Сблокированная схема.
Надежность системы без резервирования составит:
Таким образом, система без резервирования является на 28% менее надежной, чем система с резервированием.
Источник