Потеря равновесия при ремонте крыши задача по физике

§ 52. Примеры решения задач по теме «Равновесие твёрдых тел»

При решении задач статики надо использовать условия равновесия (7.9). Причём от векторного уравнения для суммы сил следует перейти к проекциям сил на координатные оси. Иногда удобнее решать задачу, используя геометрическое правило сложения векторов. При равновесии многоугольник сил должен быть замкнутым, так как сумма сил равна нулю (подобный пример будет рассмотрен ниже).

При записи для правила моментов сил надо подумать, как выбрать ось, чтобы плечи сил определялись наиболее просто и в сумме моментов сил содержалось меньше слагаемых.

В задачах часто рассматриваются стержни, которые скрепляются шарнирно. При этом имеется в виду, что трение в шарнире отсутствует.

Задача 1. Груз висит на двух тросах (рис. 7.5, а). Угол АСВ равен 120°. Сила тяжести, действующая на груз, равна 600 Н. Определите силы натяжения тросов АС и СВ.

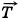
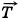
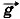
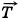
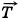
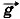
Р е ш е н и е. Силы натяжения тросов обозначим через ₁ и ₂. Эти силы направлены вдоль тросов от точки С (рис. 7.5, б). Кроме этих сил, на точку С действует сила тяжести m. Точка С находится в равновесии. Следовательно, сумма сил, действующих на неё, равна нулю:

₁ + ₂ + m = 0.

Оси координат выберем так, как показано на рисунке (7.5, в). При равновесии сумма проекций всех сил на оси координат равна нулю:

Т₂ = T₁cos60° ≈ 345 Н.

Задача 2. Дверь люка АО, которая может поворачиваться в шарнире О без трения, удерживается в горизонтальном положении верёвкой (рис. 7.6, а). Определите натяжение верёвки и силу реакции шарнира, если верёвка образует с дверью угол α = 60°. Дверь однородна и на неё действует сила тяжести 300 Н.

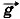
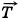
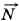
Р е ш е н и е. На дверь люка действуют три силы (рис. 7.6, б): сила тяжести m, приложенная к середине двери в точке D, сила натяжения со стороны верёвки и сила реакции со стороны шарнира.

Выберем оси координат так, как показано на рисунке (7.6, б). Поскольку дверь находится в равновесии, то сумма моментов всех сил относительно, например, шарнира равна нулю: М₁ + М + М₂ = 0.

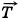
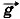
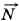
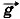
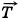
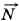
Здесь M₁, М, М₂ — моменты сил , m и . Найдём плечи этих сил, обозначив |АО| = l. Тогда OD = l/2 — плечо силы m, СО = AOsinα = lsinα — плечо силы . Плечо силы равно нулю, так как она приложена в шарнире.

Значит, М₁ = -Tlsinα, М₂ = 0.

Теперь запишем правило моментов сил, учитывая знаки этих моментов:

Отсюда находим силу натяжения верёвки:

Для нахождения силы реакции шарнира воспользуемся первым условием равновесия:

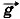
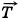
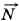
m + + =0.

Запишем это векторное уравнение в проекциях на координатные оси:

или N_х = Тcosα,

Отсюда N_х = 86,5 H; N_хy = 150 H.

Модуль силы N равен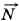

Угол, который образует сила 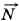с координатной осью OY:

Задача 3. Лестница прислонена к стене. При каком минимальном угле наклона к полу она не будет падать? Коэффициенты трения между лестницей и стеной и между лестницей и полом соответственно равны μ₁ и μ₂.

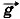
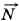
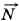
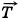
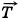
Р е ш е н и е. На лестницу действуют следующие силы (рис. 7.7): тяжести m, нормальной реакции со стороны стены ₁ и пола ₂, трения _тр1 и _тр2.

Первое условие равновесия для лестницы имеет вид

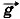
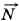
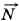
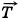
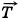
m + ₁ + ₂ + _тр1 + _тр2 = 0. (1)

Для записи правила моментов выберем ось вращения, проходящую через точку С, и запишем:

Из последнего уравнения следует:

Выразим силы N₁ и F_тp1 через силу тяжести. Для этого запишем уравнение (1) в проекциях на оси координат:

на ось X: N₁ — F.rp2 = О,
на ось Y: F_тp1 + N₂ — mg = 0.

По условию задачи требуется найти минимальное значение угла amin, поэтому берём максимальные значения сил трения, т. е. F_тp1 = μ₁N₁, и F_тp2 = μ₂N₂

Тогда

Задачи для самостоятельного решения

1. Для запуска планера применяют резиновый канат. Определите силу, с которой планер действует на канат, в тот момент, когда две половины каната составляют между собой угол 90°, а каждая из них растянута силой 500 Н.

2. К концу рукоятки гаечного ключа длиной 20 см приложена сила 50 Н под углом 60° по отношению к рукоятке ключа. Определите момент этой силы.

3. Человек, открывая дверь, прикладывает силу 4 Н, которая направлена под углом 60° к плоскости двери в горизонтальном направлении. Момент силы равен 3,5 Н • м. Определите расстояние от ручки до оси вращения двери.

4. Труба массой 14 кг лежит на земле. Какую силу надо приложить к одному из концов трубы, чтобы его слегка приподнять?

5. На трапеции сидит гимнаст массой 60 кг. Он расположен на расстоянии 1/3 её длины, считая от одного из её концов. Определите натяжение тросов, на которых подвешена трапеция.

Повторите материал главы 7 по следующему плану

1. Выпишите основные понятия и физические величины и дайте им определение.

2. Сформулируйте законы и запишите основные формулы.

3. Укажите единицы физических величин и их выражение через основные единицы СИ.

4. Опишите основные опыты, подтверждающие основные закономерности.

«Статика — частный случай динамики»

1. Различные виды равновесия тел. Эксперименты, показывающие равновесие тел. Гимнаст на канате.

2. Центр тяжести и центр масс. Экспериментальное определение центра тяжести.

Источник

Задачи для закрепления темы «Равновесие тел», 7 класс.

Самостоятельная работа (15 мин.) или фронтальный опрос в классе.

Задачи для закрепления темы «Равновесие тел», 7 класс.

(задание можно дать на дом,используя дистанционные образовательные платформы).

1.Каким специальностям необходимы знания о равновесии тел? Проектировщикам и конструкторам различных сооружений (высотных зданий, мостов, телевизионных башен и т.д.), цирковым артистам, водителям и другим специалистам

2.Почему «Ванька-встанька» возвращается в положение равновесия при любом наклоне

игрушки? ( Центр тяжести у игрушки ванька — встанька расположен очень низко, игрушка находится в устойчивом равновесии).

3. Почему Пизанская башня стоит под наклоном и не падает? ( Линия вдоль которой действует сила тяжести проходит через площадь основания ПИЗАНСКОЙ БАШНИ поэтому башня находится в состоянии устойчивого равновесия).

А) У них тяжелый труд все время, что-то жмут? (тиски)

Б) Две сестры качались, правды добивались, а когда добились, то остановили(весы).

Это Воваэто Саша. Его вес 300 Н

Это Вова. Нужно найти его вес.

1. Сидя на стуле, выпрямить спину, ноги поставить под углом 90о. Не наклоняя корпус вперед, и не двигая ноги под стул, попробуйте встать.

2. Попробуйте встать со стула, наклоняясь вперед.

3. Широко расставив ноги.

4. Сделайте соответствующие выводы.

Ответ. Учащиеся делают выводы о том, что для того чтобы встать необходимо, чтобы отвесная линия пересекала площадь опоры человека.

Пояснение, которое может дать учитель после проверки: центр тяжести тела человека находится примерно на 20 — 23 сантиметра ниже пупка. Воображаемая линия, проведённая отвесно из центра тяжести, проходит ровно между ступнями. Площадь опоры при вертикальном положении человека ограничена тем пространством, которое находится под подошвами и между стопами. Центральная точка отвесной линии центра тяжести на стопе находится на 5 см впереди от пяточного бугра

Источник