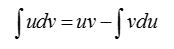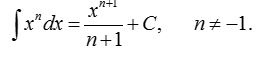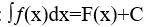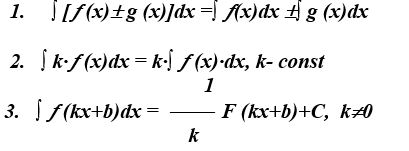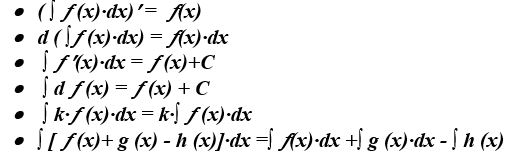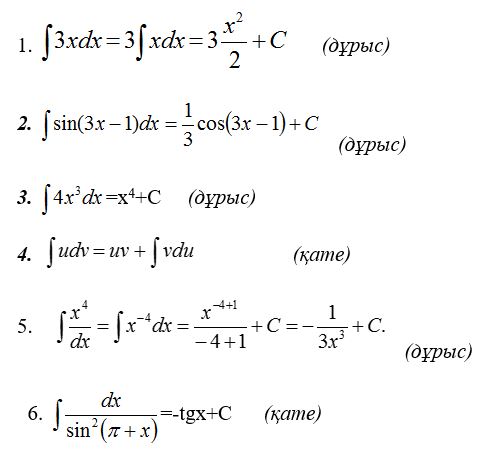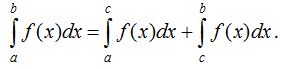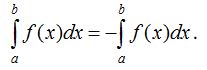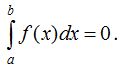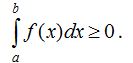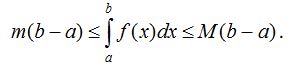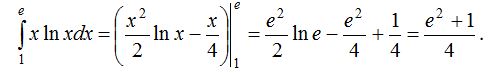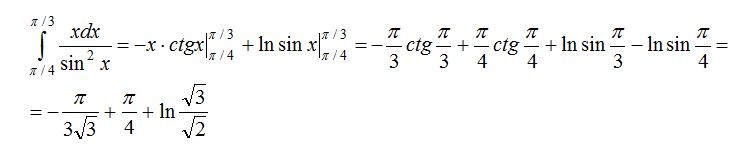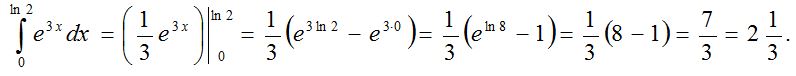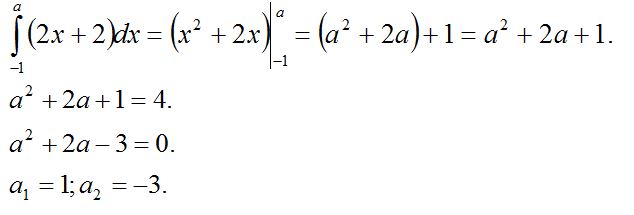Анықталған интегралды есептеу
Көптеген математикалық құбылыстарды моделдеу анықталған интегралдарды есептеуді талап етеді. Сандық әдістер теориясынан интегралдарды жуықтап есептеу үшін Трапеция және Симпсон әдістері қолданылатыны белгілі.
MatLab-та трапеция әдісі үшін trapz функциясы қолданылады:
Бұл функцияны қолдану үшін аргументтің (х-тің) мәндерін және оларға
сәйкес функцияның (у-тің) көрінісін беру керек.
Мысалы: 
интегралды есептелік:
Мұнда алынған нәтеже х-тің өзгеру қадамына (мысалда 0,1-ге тең) байланысты болады, нәтиже дәлірек шығу үшін қадам кіші болу керек.
Ал интегралды есептеудің екінші – Симпсон әдісінде оны көрсетудің қажеті жоқ. Оны MatLab өзі есептейді. Мұнда 
интегралды есептеу үшін quad(‘f’,a,b) функциясы қолданылады. Бірақ мұнда f(x) функцияны, егер ол элементарлық функция болмаса, алдын-ала MatLab-та сақтап қою керек, мысалы, fun1.m файлында интегралды есептеу үшін sinx∙e -x функцияны төмендегіше сақтаймыз:
0.5023 нәтижені аламыз.
М-файлдар
MatLab командасы топтарының ең ыңғайлы тәсілі М-файлдарды қолдану болып табылады. Оларда команда жинауға болады, олардың бәрін бірден немесе бөлімдермен орындауға болады, файлда сақтауға және бұдан былай қолдануға болады. М-файлдармен жұмыс істеу үшін М-файлдар редакторы арналған. Оның көмегімен өзіңнің функцияңды құруға және оларды шақыруға болады, сонымен қатар командалық терезеден де шақыруға болады. MatLab негізгі терезесінен Fileмәзірін ашыңыз жәнеNew пунктінен M-fileподпунктін таңдаңыз. М-файл редакторлар терезесінен жаңа файл ашылады, ол келесі суретте бейнеленген. М-файлдың ашылуы жұмыс ортасындағы File менюіндегі Open пункті көмегімен орындалады, немесе М-файлдар редакторы көмегімен орындалады.
MatLab-та М-файлдар екі типті болады: файл-программалар (Script M-Files), командаларды жүйелі түрде ұстаушы, және файл-функция, (Function M-Files), пайдаланушылармен анықталатын функциялар жазылады.
Көп жағдайда MatLab-тың жұмысшы ортасында белгілі бір жұмыстарды атқару үшін көптеген командаларды ендіру қажет болады. Ал оларды келесі жолы тағы көрсету қажет болса, сол командаларды тағы да ендіру қажет болады. Бұл тек қана көп уақытты алып қана қоймай, қателіктер жіберуге де келіп соғуы мүмкін. Демек, сол командаларды сақтап қою қажеттігі туады. MatLab-та сондай құрал сценарий деп аталады. Сценарий дегеніміз мәтіндік файл болып, онда жоғарыда айтылған, орындалуы тиіс болған. MatLab командалары жазылған болады және міндетті түрде ол файлдың кеңейтілмесі бірғана m әрпінен тұруы тиіс. Сол себепті мұндай файл М-файл деп аталады.
М-файлда кез келген мәтіндік редакторда жазуға болады. Бірақ MatLab-та мұның үшін арнайы редактор бар және онда жұмыс істеу қолайлы. Себебі ол MatLab-тың арнайы функциялары мен сөздерін басқа түспен көрсетіп тұрады және әр қатар нөмірленген болады. Ол MatLab-тың File→New→M-file мәзірлері арқылы немесе сол жақ шеттегі ақ парақ белгісін беру арқылы шақырылады.
Сценарийдің ерекшелігі – М-файлдағы және MatLab-тың жұмысшы ортасындағы айнымалылар бір бүтін жұмысшы ортаны құрайды.
Сценарий дайын болғасын оны компьютер жадына сақтау керек. Бұл m-файлды кез келген каталогта сақтау мүмкін. Дегенмен ол каталог MatLab-қа белгілі болуы тиіс. Себебі жұмысшы ортада m-файл аты жазылып, ‘Enter’ басылғанда MatLab оны іздеп табады. Жаңа каталогты жасау үшін мына команданы береміз. File→Set Path. Бұл терезеде MatLab-та тіркелген барлық каталогтар тізімге қосу үшін: Add Folder →Создать папку командасын орындаймыз. Осылайша біздің жаңа каталогымыз тізімге қосылғасын, онда m-файлымызды сақтауға болады.
Дайын болған сценарийді жұмысшы ортадан шақыру үшін тек оның атын жазып (m бөлігі жазылмайды). ‘Enter’ басу керек.
Сценарийлерді пайдаланудың артықшылығы мен бірге кемшілігі де бар: оны әр қашан бір түрлі жұмысшы ортада шақыру қажет, демек жұмысшы орта өзгерген кезде оны шақыруға және парамертлердің мәндерін ендіруге болмайды. Кез келген уақытта шақыруға болатын және жұмысшы ортаға тәуелсіз болатын файл М-функциялар деп аталады.
Бұл мәтіндегі % белгісі комментарийді білдіреді және ол тек қана пайдаланушыға мәлімет беру үшін қолданылады, оны MatLab орындамайды. Мұнда арнайы айта кететін жай – drawnow командасы. Ол тек қана сценарий немесе m-функцияда ғана қолданылады және ол сол мезетте график сызу керектігін көрсетеді. Басқаша айтқанда MatLab-тың жұмысшы ортасында жоғарыдағы командаларды берген кезде автоматты түрде графиктер сызылады. Ал сценарий мен m-функцияларда бұл командасыз өздігінен графиктер сызылмайды.
Не нашли, что искали? Воспользуйтесь поиском:
Источник
Ремонт интегралын есептеу? дістері
Шымкент аграрлық колледжі
Бедебаева Айгуль Ерсултановна
Дәрістің тақырыбы: «Анықталған интеграл және оның қасиеттері»
Дәрістің мақсаты
Білімділік: Оқушыларға анықталған интеграл ұғымы мен қасиеттерін және интегралды есептеу үшін Ньютон-Лейбниц формуласын қолдану бойынша білік, дағдыларын қалыптастыра отырып, білімдерін нақтылау.
Дамытушылық: интегралдарды есептеу кестелерін есте сақтау және оларды есептер шығаруда қолдана білуге дағдыландыру, логикалық ойлау қабілетін дамыту;
Тәрбиелік: Соңғы нәтижеге жету жолында табандылық пен жігерлілік көрсете білуге, өзін-өзі бағалай білуге тәрбиелеу.
Дәрістің түрі: Жаңа сабақты меңгерту
Оқыту әдісі: Түсіндіру, сұрақ-жауап, жүйелеу, есеп шығарту
Әдістемелік қамтамасыз етілуі:
Көрнекіліктер: Таратпа материалдары, слайдтар, плакаттар.
ОТҚ: Интерактивті тақта
Пән аралық байланыс: Физика, информатика
Қолданылатын әдебиеттер:
1. Негізгі
1.Ә.Н.Шыныбеков. Алгебра және анализ бастамалары. 11-сыныпқа арналған оқулық.Алматы «Атамұра» 2007ж
2.А.Әбілқасымова Алгебра және анализ бастамалары 11 Алматы «Мектеп» 2007ж.
2. Қосымша
1. П.Т.Апанасов, М.И.Орлов Сборник задач по математике Москва 1987г.
2. Н.В.Богомолов. Практические занятия по математике. Москва «Высшая школа» 1990г.
Дәрістің құрылымы мен мазмұны
І. Ұйымдастыру кезеңі:
1. Оқушыларды түгелдеу, дәрісхана тазалығын тексеру, оқушылардың сабаққа дайындығын бақылай отырып, зейінін сабаққа аудару.
2. Өткен білімдерге сүйене отырып, оқу әрекетін дамыту
ІІ. Үй тапсырмасын сұрау: Интегралдарды есептеудің негізгі әдістері.
«Есіңде ме, формула» – үй тапсырмасын қайталау, сұрақ-жауап
1. Тікелей интегралдау әдісі дегеніміз не?(5 ұпай)
Тікелей интегралдау әдісі дегеніміз берілген интегралды ешқандай әдістерді қолданбай тікелей интегралдау формуласына салып шығару.
2. Айнымалы ауыстыру әдісі дегеніміз не?Мысал келтір. (10 ұпай)
3. Қандай интегралдық есептерде бөліктеп интегралдау әдісін қолданамыз? (15 ұпай)
Көбейтінді түрде берілген екі функцияны интегралдауда қолданамыз.
4. х n -ның интегралы (5 ұпай)
5.a n -ның интегралы (10 ұпай)
6. 
-тың интегралы (15 ұпай)
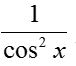
7. Анықталмаған интеграл дегеніміз не? (5 ұпай)
Анықтама: Берілген аралықтағы F(х) функциясының алғашқы функциясы осы аралықтағы f(х) функциясының анықталмаған интегралы деп аталады.
Белгіленуі: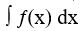 
икстен эф де икс функциясының анықталмаған интегралы деп оқылады)
Анықтамаға сәйкес: 
Мұндағы: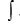 
— интеграл таңбасы
f(х) – интеграл астындағы функция
f(х) dx – интеграл астындағы өрнек
х- интегралдау айнымалысы
C- кез-келген тұрақты шама
8. Интегралдау ережелері: (10 ұпай)
9. Анықталмаған интеграл қасиеттері: (15 ұпай) 
«Қатесін тап» ойыны- үй тапсырмасын қайталау (3 ұпай)
ІІІ. Жаңа сабақ:
Жаңа сабақтың жоспары
1. Анықталған интеграл қасиеттері
2. Ньютон-Лейбниц формуласы
3. Мысалдар келтіру
4. «Жасырын суретті анықтау»
5. «Сиқырлы сандықша»
6. Қорытынды: оқушыларды үй тапсырмасына және жаңа сабаққа қатысуы барысында алған ұпайлары бойынша бағалау.
Жаңа материалды түсіндіру.
1. F(b) — F(a) айырмасын y=f(x) функциясының [a;b] кесіндісіндегі анықталған интегралы деп атайды.
Мұндағы a және b сандары интегралдау шектері: a – төменгі шегі, ал b – жоғарғы шегі.
Анықталған интегралдың негiзгi қасиеттерi.
Берiлген анықталған интегралдың бар болу шарты орындалады деп есептейiк.
1 0 . Тұрақты санды анықталған интеграл белгiсiнiң алдына шығаруға болады:
,
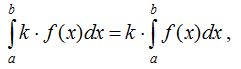
2 0 . Бiрнеше функциялар қосындысының анықталған интегралы қосылғыштарының анықталған интегралдарының қосындысына тең:
.
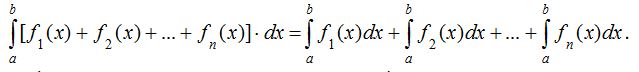
Осы екi қасиет интегралдың сызықтық қасиетi деп аталады.
3 0 . Егер [a;b] аралығын [a;c] және [c;b] аралықтарына бөлсек, онда
4 0 . Егер интегралдың жоғарғы шегi мен төменгi шегiнiң орындарын ауыстырсақ, онда оның таңбасы өзгередi:
5 0 . Жоғарғы шегi мен төменгi шегi тең болатын интеграл 0-ге тең
6 0 . Егер [a;b] аралығындағы х айнымалысының барлық мәндерi үшiн 
болса, онда
7 0 . Егер [a;b] аралығындағы х айнымалысының барлық мәндерi үшiн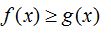 
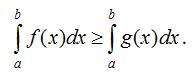
болса, онда
.
8 0 . Егер [a;b] аралығында функциясының ең үлкен және ең кiшi мәндерi сәйкес М және m сандары болса, онда 
2. Ньютон-Лейбниц формуласы.
Ньютон Исаак (1643-1727) — ағылшын астрономы, физигі, әрі математигі. ХVII ғасырда дифференциалдық және интегралдық есептеулерді математикалық практикаға енгізді.
Туындыны дифференциалдау деп атаған және интеграл белгісін енгізген Лейбниц
Готфрид Вильгельм Лейбниц (1646-1716 жж.) – XVII ғасырдағы неміс рухы туғызған терең де жан-жақты дамыған философ. Екінші жағынан, ол — математик, физик, саясаткер, тарихшы, құқықтанушы.
Теорема. Егер F(X) функциясы [a;b] аралығына f(x) функциясының алғашқы функциясының бiрi болса, онда
(5)
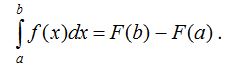
Бұл теңдiк Ньютон-Лейбниц формуласы деп аталады.
Анықталған интегралдарға байланысты мысалдар келтіру.
1-есеп.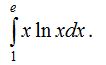 
.
Интеграл астындағы функцияның алғашқы функциясын бөлiктеп интегралдау әдiсiмен тауып және оған Ньютон-Лейбниц формуласын қолдансақ,
2-есеп.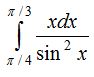 
.
Бөліктеп интегралдау формуласы бойынша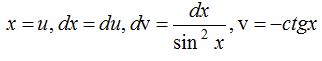 
болса, онда
3-есеп.
4-есеп.
ІV. Жаңа сабақты бекіту: «Жасырын суретті анықта » ойыны (ұяшықтарға жасырылған есептерді шығару арқылы, астындағы суретте кім бейнеленгенін анықтау қажет)
Лайықтап жазылған ұпайлары,
Интегралға есеп бар мұнда тағы Алғашқы функциясын табарсың, қателеспей,
Жетерлік болса егер білім жағы.
«Сиқырлы сандықша» (сандықша ішіндегі есептерді шығару)
“Алгебра және анализ бастамалары, 11 сынып, А.Е.Әбілқасымова, 23-24 бет”
Есіңде ме формула
Ойлан тап!
Жасырын суретті анықтау
Сиқырлы сандықша
Жалпы ұпайы
6-10 ұпай жинаған оқушылар 3 деген бағамен бағаланады
11-20 ұпай жинаған оқушылар 4 деген бағамен бағаланады
20 ұпайдан жоғары жинаған оқушылар 5 деген бағамен бағаланады.
Источник