Среди 700 предприятий занимающихся ремонтом радиотехнической аппаратуры

ID работы — 638166
математика (контрольная работа)
количество страниц — 15
год сдачи — 2012

1. В урне 10 шаров, из которых 2 белых, 3 черных и 5 синих. Наудачу извлечены 3 шара. Какова вероятность того, что все 3 шара разного цвета
2. Из 18 стрелков 5 попадают в мишень с вероятностью — 0,7; 8 с вероятностью 0,6 и 5 с вероятностью 0,5. Наудачу выбранный стрелок не попал в мишень. К какой группе вероятнее всего принадлежит этот стрелок
3. Найти математическое ожидание, дисперсию и вероятность попадания в интервал (3; 4)
4. Найти вероятность того, что при n испытаниях событие наступлений равно k раз
5. Дана вероятность p появления события А в каждом из n независимых испытаний, найти вероятность того, что в этих испытаниях событие А появится не менее k1 и не более k2 раз
6. Задан закон распределения дискретной случайной величины Х. Найти: 1. Математическое ожидание М(Х); 2. Дисперсию D(X); 3. Cреднее квадратическое отклонение ?
7. Среднее квадратическое отклонение нормально распределенной случайной величины равно 0,5. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине не превосходит 1
8. Среди 700 предприятий, занимающихся ремонтом радиотехнической аппаратуры в некотором регионе, по схеме собственно-случайной безповторной выборки отобрано 60. Получено следующее распределение предприятий по числу заказов в неделю
9. По данным задачи 8, используя критерий Пирсона, при уровне значимости — 0,05 проверить гипотезу о том, что случайная величина Х — число заказов в неделю распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирических и теоретических частот

1. В урне 10 шаров, из которых 2 белых, 3 черных и 5 синих. Наудачу извлечены 3 шара. Какова вероятность того, что все 3 шара разного цвета.
Число всех возможных событий, равна числу способов, которыми можно взять 3 шара из 10, и равна числу сочетаний с 10 элементов по 3

Источник

Указания по выполнению контрольных работ 2 страница

Вариант 5

Контрольная работа №1

В коробке — 4 красных карандаша, 5 — синих и 6 — зеленых. Наудачу извлекаются три карандаша. Найти вероятность того, что: а) среди них не менее двух зеленых; б) все карандаши разных цветов.

При установившемся технологическом процессе изготавливается в среднем 15% бракованных шин. Сколько шин нужно взять для проверки, чтобы с вероятностью 0,9876 доля бракованных шин оказалась бы в границах от 0,1 до 0,2?

Полоса препятствий некоторых соревнований содержит три рубежа различной сложности. Спортсмен преодолевает эти рубежи без штрафных очков с вероятностями 0,7, 0,4 и 0,2 соответственно. Составить закон распределения случайной величины Х — числа рубежей полосы препятствий, пройденных без штрафных очков. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины.

Случайная величина X нормально распределена, причем P(Х>2)=0,5 и P(Х£3,3) = 0,9032. Найти M(Х), D(X), P(1£Х£4).

Сколько раз нужно измерить температуру раствора, чтобы с вероятностью не менее 0,95 можно было утверждать, что средняя арифметическая этих измерений будет отличаться от истинного значения температуры раствора не более чем на 2°C (по абсолютной величине), если среднее квадратическое отклонение измерений — не более чем 8°C?

Контрольная работа №2

Менеджер компании, занимающейся прокатом автомобилей, хочет оценить среднюю величину пробега одного автомобиля в течение месяца. Из 280 автомобилей, принадлежащих компании, по схеме собственно-случайной бесповторной выборки отобрано 60. Результаты представлены в таблице:

Пробег (км)	Менее 1000	1000-2000	2000-3000	3000-4000	4000-5000	6000-7000	Более 7000	Итого
Число автомобилей

а) вероятность того, что средний пробег автомобиля в месяц отличается от среднего их пробега в выборке не более чем на 400 км (по абсолютной величине);

б) границы, в которых с вероятностью 0,95 заключена доля автомобилей, пробег которых составляет менее 3000 км;

в) объем бесповторной выборки, при котором те же границы для указанной доли можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных сведений о рассматриваемой доле нет.

По данным задачи 1, используя критерий

-Пирсона, при уровне значимости

проверить гипотезу о том, что случайная величина Х — пробег автомобиля в месяц — распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

Распределение 70 предприятий по себестоимости единицы изделия Х (тыс. руб.) от выпуска продукции Y (тыс. шт.) представлено в таблице:

x\y	2,2-2,4	2,4-2,6	2,6-2,8	2,8-3,0	3,0-3,2	3,2-3,4	Итого
0,5-1,5
1,5-2,5
2,5-3,5
3,5-4,5
4,5-5,5
5,5-6,5
Итого

1) вычислить групповые средние и , и построить эмпирические линии регрессии;

2) предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:

а) найти уравнения прямых регрессии и построить их графики на одном чертеже с эмпирическими линиями регрессии;

б) вычислить коэффициент корреляции на уровне значимости , оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;

в) используя соответствующее уравнение регрессии, определить количество выпускаемой продукции при стоимости одной единицы продукции, равной 2,5 тыс. руб.

Вариант 6

Контрольная работа №1

Пряжа поступает с трех станков, производительности которых относятся как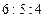

. Вероятность того, что поступившая с первого станка пряжа будет высшего качества, равна 0,2, со второго — 0,3. Найти вероятность изготовления пряжи высшего качества на третьем станке, если среди продукции всех трех станков доля пряжи высшего качества равна 0,32.

Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность: а) попадания в цель при одном выстреле; б) менее трех попаданий при четырех выстрелах.

Вероятность появления газовых раковин при отливке блока цилиндров автомобильного двигателя равна 0,1. Изготовлено 400 блоков цилиндров. Найти наибольшее отклонение частости отлитых блоков цилиндров с наличием газовых раковин от вероятности 0,1, которую можно гарантировать с вероятностью 0,9963.

При первичной поломке прибора, которая возможна с вероятностью 0,2, прибор ремонтируется. При вторичной поломке, происходящей с вероятностью 0,5, прибор снимается с испытаний. Составить закон распределения случайной величины Х — числа приборов снятых с испытаний из трех проверяемых. Найти математическое ожидание и дисперсию этой случайной величины.

в остальных случаях

При каком значении параметра

функция

является плотностью распределения вероятности некоторой непрерывной случайной величины X? Найти вероятность того, что при двух измерениях этой случайной величины в обоих случаях ее значения будут принадлежать интервалу (-1; 1).

Контрольная работа №2

Среди 700 предприятий, занимающихся ремонтом радиотехнической аппаратуры в некотором регионе, по схеме собственно-случайной бесповторной выборки отобрано 60. Получено следующее распределение предприятий по числу заказов в неделю:

Число заказов в неделю	Менее 80	80-100	100-120	120-140	140-160	160-180	Более 180	Итого
Количество предприятий

а) границы, в которых с вероятностью 0,9 заключено среднее число заказов в неделю для указанных предприятий данного региона;

б) вероятность того, что доля предприятий в регионе, у которых число заказов в неделю больше 140, отличается от доли таких предприятий в выборке не более чем на 0,05 (по абсолютной величине);

в) объем бесповторной выборки, при котором те же границы для среднего числа заказов в неделю для всех рассматриваемых предприятий можно гарантировать с вероятностью 0,95.

По данным задачи 1, используя критерий

-Пирсона, при уровне значимости

проверить гипотезу о том, что случайная величина Х — число заказов в неделю — распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

Распределение 100 работников компании по результатам тестирования Х (баллы) и показателям работы Y (баллы) представлено в таблице:

x\y	5-6	6-7	7-8	8-9	9-10	Итого
9-11
11-13
13-15
15-17
17-19
19-21
Итого

1) вычислить групповые средние и , и построить эмпирические линии регрессии;

2) предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:

в) используя соответствующее уравнение регрессии, определить результат тестирования работников, у которых показатель работы равен 8 баллам.

Вариант 7

Контрольная работа №1

На карточках написаны буквы, образующие слово “КОМБИНАТОРИКА”, две карточки из этого набора утеряны. Наудачу извлекается одна карточка. Какова вероятность того, что на ней окажется гласная буква?

Одновременно бросаются три игральные кости. Найти вероятность того, что сумма выпавших очков будет не менее 16-ти.

Вероятность того, что прибор, случайно выбранный из партии, нуждается в дополнительной регулировке, равна 0,05. Если при выборочной проверке обнаруживается, что не менее 6% отобранных приборов нуждаются в регулировке, то вся партия будет возвращена для доработки. Найти вероятность того, что партия будет возвращена, если контролю будет подвергнуто 500 приборов из этой партии.

Имеется пять ключей, из которых два подходят к замку. Составить закон распределения числа Х проб при открывании замка, если использованный ключ в последующих пробах не участвует. Найти функцию распределения случайной величины X, ее математическое ожидание и дисперсию.

в остальных случаях

Плотность распределения непрерывной случайной величины Х имеет вид:

, где a > 0. Найти значения параметра a, если M(Х) = 1. Вычислить P(Х> 2).

Контрольная работа №2

По схеме собственно-случайной бесповторной выборки в некотором промышленном регионе из 200 котельных обследованы 50. Получены следующие данные о числе дней, в течение которых котельные обеспечены топливом:

Число дней	Менее 6	6-12	12-18	18-24	24-30	Более 30	Итого
Число котельных

а) вероятность того, что среднее число дней, в течение которых котельные обеспечены топливом, во всем регионе отличается от среднего числа дней в выборке не более чем на 2 дня (по абсолютной величине);

б) границы, в которых с вероятностью 0,95 заключена доля тех котельных во всем регионе, которые обеспечены топливом менее чем на 12 дней;

в) объем бесповторной выборки, при котором те же границы для доли котельных во всем регионе можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных сведений о рассматриваемой доле нет.

По данным задачи 1, используя критерий

-Пирсона, при уровне значимости

проверить гипотезу о том, что случайная величина Х — количество дней, в течение которых котельные обеспечены топливом, — распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

Распределение 50 компаний, занимающихся грузовыми перевозками, по количеству машин X (ед.) и среднемесячным доходом Y (млн. руб.) представлено в таблице:

x\y	70-75	75-80	80-85	85-90	90-95	Итого
20-30
30-40
40-50
50-60
60-70
Итого

1) вычислить групповые средние и , и построить эмпирические линии регрессии;

2) предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:

б) вычислить коэффициент корреляции на уровне значимости a = 0,05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;

в) используя соответствующее уравнение регрессии, определить среднемесячный доход компаний, имеющих 40 машин.

Закон распределения случайной величины Х имеет вид:

Вариант 8

Контрольная работа №1

Из 12 акций 3 принадлежат первому предприятию, 4 — второму и 5 — третьему. Пусть X, Y, Z — числа акций соответственно первого, второго и третьего предприятий среди двух акций, случайно отобранных из общего числа. Найти вероятность

. Выяснить, являются ли события (Х=1) и (Y=1) независимыми.

При данном технологическом процессе в среднем k% изделий удовлетворяют стандарту. Найти вероятность того, что в партии из n изделий будет: а) 40 бракованных, если k = 80%, n = 200; б) менее 3-х бракованных, если k = 99,2%, n = 100.


	0,3	0,7

Случайная величина Y имеет биномиальное распределение с параметрами n = 2, p = 0,4.

Составить закон распределения случайной величины Z = 2Х + Y, полагая, что Х и Y — независимы.

Функция распределения непрерывной случайной величины Х имеет вид: F(x) =

где а и b — некоторые числа. Найти значения параметров а и b, если P(Х > 1) = 1/8. Вычислить P(1£X£ 2). Средний расход воды на животноводческой ферме составляет 1000 л в день, а среднее квадратическое отклонение этой случайной величины не превышает 200 л. Оценить вероятность того, что расход воды на ферме в наудачу избранный день не превысит 2000 л, используя: а) лемму Чебышева (неравенство Маркова); б) неравенство Чебышева. Контрольная работа №2 По схеме собственно-случайной бесповторной выборки в некотором крупном городе проводилось исследование количества вызовов скорой помощи в сутки. За последние три года отобраны 90 дней. Результаты представлены в таблице:

Число вызовов	Менее 400	400-500	500-600	600-700	700-800	800-900	Более 900	Итого
Количество дней

а) вероятность того, что среднее число вызовов в день за указанный период времени отличается от среднего их количества в выборке не более чем на 25 (по абсолютной величине);

б) границы, в которых с вероятностью 0,95 заключена доля тех дней за рассматриваемый период, в которых количество вызовов было не менее 700;

По данным задачи 1, используя критерий

-Пирсона, при уровне значимости

проверить гипотезу о том, что случайная величина Х — количество вызовов в день — распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую. 3. Распределение 60-ти образцов сырья по процентному содержанию в них минерала X (%) и минерала Y (%) представлено в таблице:

x\y	10-12	12-14	14-16	16-18	18-20	Итого
20-30
30-40
40-50
50-60
60-70
Итого

1) вычислить групповые средние и , и построить эмпирические линии регрессии;

2) предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:

в) используя соответствующее уравнение регрессии, определить процентное содержание минерала Х в сырье, содержащем 18% минерала Y.

Вариант 9

Контрольная работа №1

При первом выстреле вероятность попадания первого стрелка в движущуюся мишень равна 0,8, второго — 0,9. При втором выстреле эта вероятность уменьшается на 0,2 для каждого стрелка. Найти вероятность того, что в мишени будет не менее двух пробоин, если каждый из стрелков сделал два выстрела.

Найти такое число k, чтобы с вероятностью 0,9 можно было бы ожидать, что среди 900 новорожденных будет не менее k мальчиков. Вероятность рождения мальчика принять равной 0,515.

В коробке среди пяти деталей — две окрашенные. Детали извлекаются последовательно до извлечения обеих окрашенных деталей (после чего извлечения прекращаются). Составить закон распределения случайной величины X — числа извлеченных деталей. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины.

Функция распределения непрерывной случайной величины X имеет вид F(х)=

. Найти вероятность того, что при трех измерениях этой случайной величины в двух случаях ее значения будут принадлежать отрезку [0; 2].

Вероятность своевременной оплаты телефонной квитанции равна 0,85. Оценить вероятность того, что из 50 квитанций число своевременно оплаченных будет: а) от 39 до 46; б) не менее 45.

Контрольная работа №2

Коробки с шоколадом упаковываются автоматически. По схеме собственно-случайной бесповторной выборки взято 130 из 2000 упаковок, содержащихся в партии, и получены следующие данные об их весе:

Вес упаковки (гр.)	Менее 975	975-1000	1000-1025	1025-1050	Более 1050	Всего
Число упаковок

а) границы, в которых с вероятностью 0,9901 заключен средний вес упаковок в партии;

б) вероятность того, что доля упаковок, вес которых менее 1000 г, во всей партии отличается от доли таких упаковок в выборке не более чем на 0,05 (по абсолютной величине);

в) объем бесповторной выборки, при котором те же границы для среднего веса упаковок во всей партии можно гарантировать с вероятностью 0,95.

По данным задачи 1, используя критерий

-Пирсона, при уровне значимости

проверить гипотезу о том, что случайная величина Х — вес упаковок — распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

Распределение 50 компаний по ежемесячным затратам на рекламу Х (тыс. руб.) и объему выручки от продаж Y (млн. руб.) представлено в таблице:

x\y	28-32	32-36	36-41	40-44	44-48	48-52	Итого
2.0-2.2
2.2-2.4
2.4-2.6
2.6-2.8
2.8-3.0
Итого

1) вычислить групповые средние и , и построить эмпирические линии регрессии;

2) предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:

в) используя соответствующее уравнение регрессии, оценить средний объем выручки от продаж при ежемесячных затратах на рекламу в размере 2,4 тыс. руб.

studopedia.org — Студопедия.Орг — 2014-2021 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.009 с) .

Источник