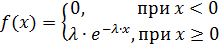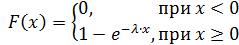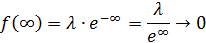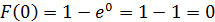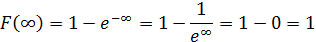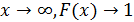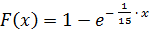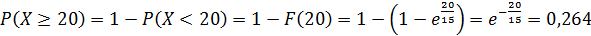Показательный (экспоненциальный закон распределения).
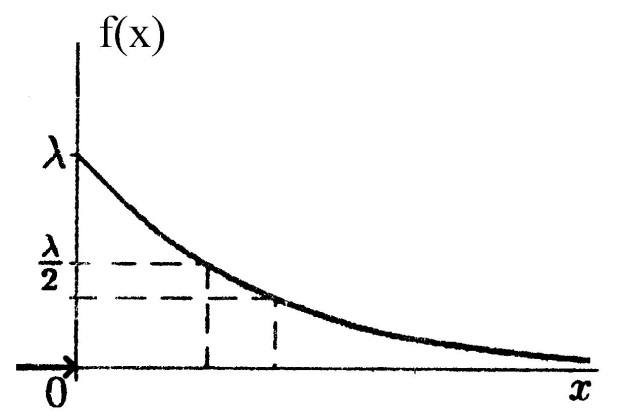
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
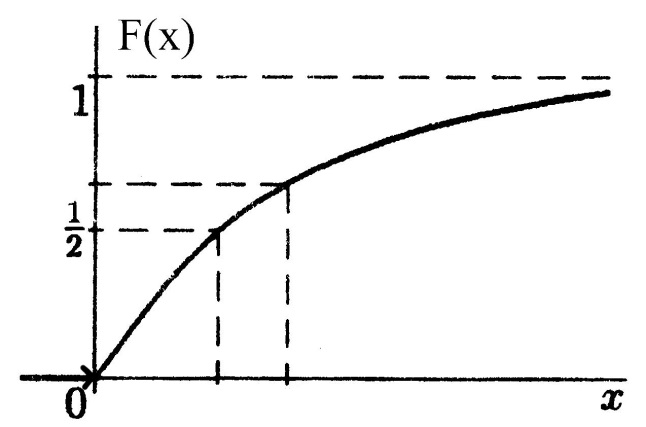
Функция распределения имеет вид:
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
, 
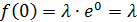
То есть при 
Пример.
Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется не менее 20дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.
Решение:
По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:
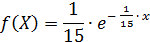
Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть
но проще это сделать, используя функцию распределения:
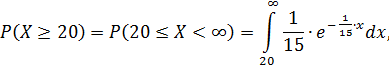
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.
Источник
Показательный (экспоненциальный закон распределения)
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
Функция распределения имеет вид:
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
То есть при 
Пример.
Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.
Решение:
По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:
Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть
но проще это сделать, используя функцию распределения:
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.
Равномерный закон распределения.
Непрерывная случайная величина Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, то есть
Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.
Дисперсия имеет вид:
Найдем вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал 
, принадлежащий целиком отрезку [a, b]:
Функция распределения примет вид:
Пример.
Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты.
Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.
Решение:
Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0;2] имеет равномерный закон распределения f (x)=1/2.
Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 1/4 от равной единице площади прямоугольника, т.е.
Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение:
Источник
Время ремонта автомобиля есть случайная величина
Название: Основы работоспособности технических систем. Автомобильный транспорт — учебное пособие (Атапин, В.Г)
3.3. закономерности
СЛУчЧАЙНЫХ ПРОчЦЕССОВ ИЗМЕНЕНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ АВТОМОБИЛЕЙ
(закономерности второго вида)
Общие понятия. Под влиянием условий эксплуатации, квалификации персонала, неоднородности самих изделий и их начального состояния и других факторов интенсивность и характер изменения параметра технического состояния у разных автомобилей будут различными. Если зафиксировать значение параметра, например, на уровне yд (рис. 3.3), то моменты достижения этого состояния (ресурса) lp у разных изделий будут различны, т.е. наработка на отказ будет случайной величиной и будет иметь вариацию.
В связи с этим возникает вопрос: как установить момент контроля и обслуживания изделий? Если зафиксировать определенную наработку к моменту контроля и обслуживания автомобиля l0, то неминуема вариация показателя его технического состояния и, как следствие, вариация трудоемкости и продолжительности выполнения работ по восстановлению технического состояния. Поэтому важно знать, какую трудоемкость и продолжительность учитывать и нормировать при организации технического обслуживания и ремонта.
Рис. 3.3. Вариация ресурса и технического состояния:
1 – сечение случайного процесса по параметру y; 2 – то же,
Очевидно, что решение этого вопроса во многом зависит от вариаций случайной величины. Характеристиками случайной величины х при N реализациях (числе наблюдений), как известно, являются:
среднее значение 
: 
;
при достаточно большом числе наблюдений полагают, что 
, где 
– математическое ожидание;
среднее квадратическое отклонение: 
;
дисперсия: 
;
коэффициент вариации: 
.
Если х – время t, то в соответствующих формулах вместо х записывается t.
В технической эксплуатации автомобилей различают случайные величины с малой 
, средней 
и большой 
вариацией. Фактически полученный в результате обработки экспериментальных данных, а также из литературных источников коэффициент 
служит для предварительного определения закона распределения данной случайной величины.
Помимо приведенных характеристик, важнейшими характеристиками случайной величины Х являются вероятность 
(например, вероятность безотказной работы P(t), вероятность отказа Q(t)) и плотность вероятности f(x) (например, вероятности отказа).
На практике, зная f(x), оценивают возможное число отказов r, которое может возникнуть за сравнительно небольшой интервал наработки 
. Для этого значение f(x1) умножают на число изделий N и величину интервала 
.
При N = 75 f(x1) = 0,02 тыс. км–1 и = 2 тыс. км получаем
r(x1 – x2) = 
отказа, Ответ
т.е. при эксплуатации 75 невосстанавливаемых изделий (или восстанавливаемых изделий – до первого отказа) есть основания ожидать в интервале наработки х1 – х2 появления 3 отказов и подготовиться соответствующим образом к их устранению.
Умножая значение плотности вероятности отказа f(x1) на величину интервала наработки, можно получить оценку вероятности отказа изделий в данном интервале:
. Ответ
Законы распределения случайной величины. Знание законов распределения случайных величин позволяет более точно планировать моменты проведения и трудоемкость ТО и ремонта, определять необходимое количество запасных частей и решать другие технологические и организационные вопросы. Для процесса технической эксплуатации наиболее характерны следующие законы распределения случайной величины.
1. Экспоненциальный закон распределения используется чаще всего при описании внезапных отказов (период нормальной эксплуатации – в этот период постепенные отказы еще не проявляются и надежность характеризуется внезапными отказами). Эти отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность, которая не зависит от возраста изделия (рис. 3.4):
,
где 
; mt – средняя наработка до отказа (обычно в часах).
Вероятность безотказной работы
подчиняется экспоненциальному закону распределения времени безотказной работы и одинакова за любой одинаковый промежуток времени в период нормальной эксплуатации.
Экспоненциальным законом распределения можно аппроксимировать время безотказной работы широкого круга объектов (изделий): особо ответственных машин, эксплуатируемых в период после окончания приработки и до существенного проявления постепенных отказов; машин с последовательной заменой отказавших деталей; машин вместе с электро- и гидрооборудованием и системами управления и др.
Существенное достоинство экспоненциального распределения – его простота: оно имеет только один параметр.
Если, как обычно, 
, то формула для вероятности безотказной работы упрощается в результате разложения в ряд и отбрасывания малых членов:
.
.
При экспоненциальном законе распределения коэффициент вариации
Приведем значения вероятности безотказной работы в зависимости от 
:
… 1 0,1 0,01 0,001 0,0001
Источник
