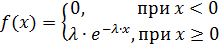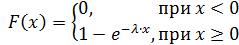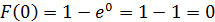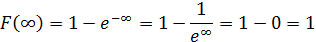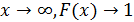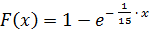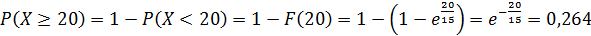Время ремонта телевизора распределено по показательному закону

Показательный (экспоненциальный закон распределения).

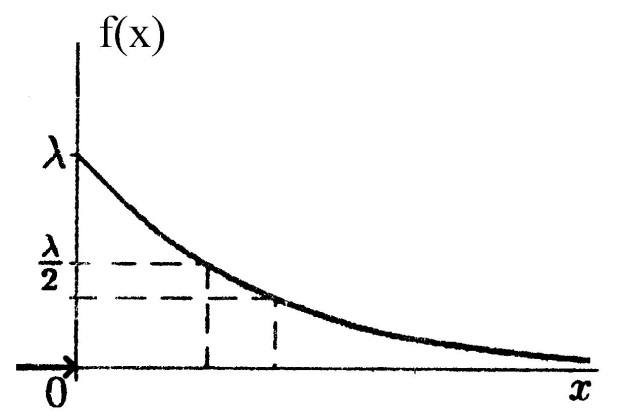
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:

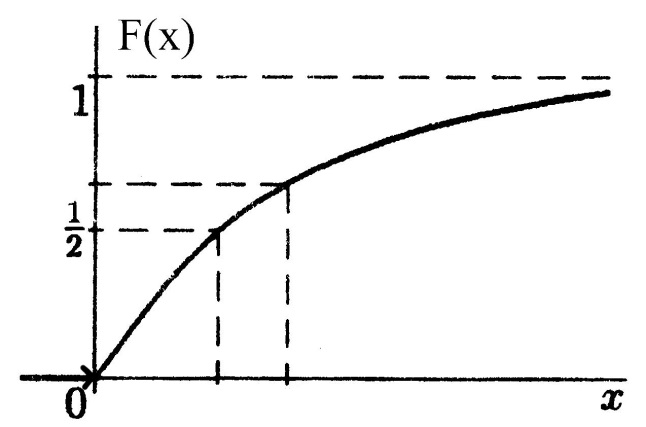
Функция распределения имеет вид:

Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:

,

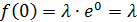
То есть при

Пример.

Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.

Определить вероятность того, что на ремонт телевизора потребуется не менее 20дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.

Решение:

По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:

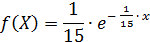
Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть

но проще это сделать, используя функцию распределения:

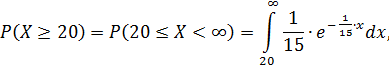
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.

Источник

Экспоненциально распределенная случайная величина

На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ — распределенных по показательному (или экспоненциальному) закону.

Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:

Функция распределения величины $X$:

Здесь $\lambda$ — единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/\lambda$, $D(X)=1/\lambda^2$.

Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $\lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.

В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.

Примеры решений

Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.

Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?

Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $\lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.

Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^<-2t>$ при $t\ge 0$ и $f(t)=0$ при $t\lt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.

Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.

Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.

Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^<-3x>$ при $x \gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.

Задача 8. Непрерывная случайная величина $\xi$ распределена по показательному закону с параметром $\lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $\xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $\xi$ и вероятность того, что $\xi$ принимает значения, меньшие своего математического ожидания.

Задача 9. Случайная величина $\xi$ распределена по показательному закону с параметром 2. Найти $M_<\xi>$, $D_<\xi>$ вероятность попадания $\xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $\xi$.

Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(\lambda)$. Найдите вероятность события $|Х — МХ | \lt 3\sigma$ («правило $3\sigma$» для показательного распределения).

Решебник по теории вероятности онлайн

Больше 11000 решенных и оформленных задач по теории вероятности:

Источник

Показательный (экспоненциальный закон распределения)

Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:

Функция распределения имеет вид:

Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:

То есть при

Пример.

Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.

Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.

Решение:

По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:

Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть

но проще это сделать, используя функцию распределения:

Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.

Равномерный закон распределения.

Непрерывная случайная величина Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, то есть

Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.

Дисперсия имеет вид:

Найдем вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал , принадлежащий целиком отрезку [a, b]:

Функция распределения примет вид:

Пример.

Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты.

Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.

Решение:

Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0;2] имеет равномерный закон распределения f (x)=1/2.

Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 1/4 от равной единице площади прямоугольника, т.е.

Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение:

Источник

Кремер Н.Ш. Теория вероятностей и математическая статистика. №004.031, стр.178

Время ремонта телевизора распределено по показательному закону с математическим ожиданием, равным 0,5ч. Некто сдает в ремонт два телевизора, которые одновременно начинают ремонтировать, и ждёт, когда будет отремонтирован один из них. После этого с готовым телевизором он уходит. Найти закон распределения времени: а) потраченного клиентом; б) которое должен потратить клиент, если он хочет забрать сразу два телевизора.

Другие задачи по теории вероятности

В лотерее разыгрываются: автомобиль стоимостью 5000 ден.ед., 4 телевизора стоимостью 250 ден.ед., 5 видеомагнитофонов стоимостью 200 ден.ед. Всего продается 1000 билетов по 7 ден.ед. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим один билет.

Вероятности того, что студент сдаст семестровый экзамен в сессию по дисциплинам А и В, равны соответственно 0,7 и 0,9. Составить закон распределения числа семестровых экзаменов, которые сдаст студент.

Дана случайная величина X:

xi	-2	1	2
pj	0,5	0,3	0,2

Найти закон распределения случайных величин: а) Y = 3X, б) Z = X 2 .

Даны законы распределения двух независимых случайных величин:

xi	0	2	4
pi	0,5	0,2	0,3

yi	-2	0	2
pj	0,1	0,6	0,2

Найти закон распределения случайных величин: а) Z=Х-Y; б) U = XY.

Вычислить М(Х) и M(Y) в задаче о стрелках. Известны законы распределения случайных величин X и Y — числа очков, выбиваемых 1-м и 2-м стрелками.

xi	0	1	2	3	4	5	6	7	8	9	10
pi	0,15	0,11	0,04	0,05	0,04	0,10	0,10	0,04	0,05	0,12	0,20

Вычислить М(Х) для случайной величины Х чистого выигрыша по данным примера 3.1: В лотерее разыгрываются: автомобиль стоимостью 5000 ден.ед., 4 телевизора стоимостью 250 ден.ед., 5 видеомагнитофонов стоимостью 200 ден.ед. Всего продается 1000 билетов по 7 ден.ед.

Найти математическое ожидание случайной величины Z=8Х-5Y+7, если известно, что М(Х)=3, М(Y)=2.

Источник